Hi readers, I hope you are all well. In this post, we discuss the main topic, equilibrium. Equilibrium can play a fundamental role in the modern and different fields of science. In physics, engineering, or also in chemistry the concept of equilibrium describes and provides information about forces that can be applied to the system. In physics, the equilibrium describes the balanced forces and the torque that can be acted on the system or the body. if the body is at rest or in a motion state, equilibrium explains and provides information about the forces that can act in both types of situations persons.
Equilibrium plays a vital role in understanding the forces and the torque because equilibrium provides stability to the system, also it stabilizes the person who is in the state of rest or motion because in both conditions forces always act on it, so for their stabilization equilibrium plays an essential role.
In this post, we can discuss the equilibrium definitions, their types, first equilibrium condition, second equilibrium condition, mathematical expressions, their applications, examples, and related phenomena.
Definition of equilibrium:
Equilibrium can be defined as:
"The state in which the body is in the state of balance, or the body is in the state of motion or rest with uniform velocity and no net change occurs on it."
Simply equilibrium is a state in which the system or the body is at the condition of balance under the action of forces but there is no net change occurring. Every system achieves equilibrium at some conditions because, without an equilibrium state, the system or the object can't do its work properly.

Types of equilibrium:
There are two main types of equilibrium which are common and they are given there:
Mechanical equilibrium
Thermal equilibrium
Their description is given there:
Mechanical equilibrium:
Mechanical equilibrium is the main type of equilibrium and it can be defined as:
In the system or an object mechanical equilibrium occurs when there is no force, torque net force, or acceleration acting on the object or the system.
Mechanical equilibrium occurs during the state of motion mostly. Mechanical equilibrium can be divided into two types which are also the main types of equilibrium and they are given below:
Static equilibrium
Dynamic equilibrium
These are the further divisions of the mechanical equilibrium Details are given there:
Static equilibrium:
Static equilibrium can be defined as:
"static equilibrium can achieved by the body when the body is at rest and all forces which can act on the body including torque and acceleration sum is equal to zero."
Dynamic equilibrium:
Dynamic equilibrium can be defined as:
"Dynamic equilibrium can be achieved by the body when the body moves with a constant velocity and the all forces and torque which can be acted on the body their sum is equal to zero."
Thermal equilibrium:
Thermal equilibrium can be defined as:
"The two objects or the two or more systems can achieve the state of thermal dynamics when no exothermic or endothermic heat exchange occurs and with some condition or time both systems can be reached to the same temperature.”
These are the major types of equilibrium but the types of equilibrium in physics are given there:
In physics the types of equilibrium:
The types of equilibrium in physics with their uses and examples are given there:
Dynamic equilibrium
Radiative equilibrium
Thermal equilibrium
Static equilibrium
Chemical equilibrium
Their detailed definitions, mathematical expressions, formulas, and examples are given there:
Dynamic equilibrium:
Dynamic equilibrium can be achieved by the body when the body moves with a constant velocity and all forces and torque which can be acted on the body their sum are equal to zero. In dynamic equilibrium all forces which can be acted on the object are balanced. Mostly dynamic equilibrium can be used to understand or determine the objects that can be moved without acceleration.
Mathematical expression:
As we know in dynamic equilibrium the all forces sum is equal to 0 then it can be written as:
F = 0
Or the sum of torque is also equal to zero, hence it can be written as:
𝛕 = 0
For instance:
The body or object can be rotated around its axis with uniform angular velocity and no acceleration can be calculated or measured and all sum of forces that can be acted are 0
The car that can be moved with uniform linear velocity on a straight road, and not change their speed then the force which can be acted to maintain the road friction or air friction can be produced through the driving force which can be produced through the engines.
The paratrooper can also fly in the sky due to the dynamic equilibrium which stabilizes them to fly in the sky efficiently.
The airplane can also fly with a state of dynamic equilibrium because it can fly with constant speed and the weight and thrust force can balance the drag force by balancing their forces it can fly efficiently.
Radiative equilibrium:
Radiative equilibrium is the state that can be achieved by the system or the object by absorbing the radiation or emitting the radiation at the same time and rate through equal emitting and absorbing radiation of the system and the object can achieved the dynamic equilibrium state efficently.
Mathematical expression:
Rate of absorption of radiation = rate of emission of radiation
For instance:
Stars can also maintain their lifecycle phase by emitting or absorbing radiation and achieving radioactive equilibrium. the stars produce energy through the nuclear fusion reaction and it can also radiate the absorbing energy into space and maintain gain radiative equilibrium.
The temperature or radiation can come from the sun and is maintained in the earth by radiative equilibrium because the earth absorbs all solar radiation and emits infrared radiation on the surface of the earth.
Thermal equilibrium:
The two objects or two or more systems can achieve the state of thermal dynamics when no exothermic or endothermic heat exchange occurs and with some condition or time, both systems can reach the same temperature. thermal equilibrium concepts are essential in thermodynamics and also in their laws.
Representation:
The temperature of the object and the system that can achieve the thermal equilibrium can represented through the symbol T.
Mathematical expression:
No heat exchange occurs in the system when they achieve the thermal equilibrium then it can be written as:
T1 = T2 = T3=........ = Tn
For instance:
For the two metal spoons, one is cold or the other is hot but if we check after some time then it can be observed that both metal spoons have the same temperature because both of them achieve thermal equilibrium.
If we leave the hot cup of tea or coffee in the room or open environment, then after some time we can observe that the hot cup of tea or coffee temperature becomes equal to the room or environment temperature,
Static equilibrium:
static equilibrium can achieved by the body when the body is at rest and all forces that can act on the body including torque and acceleration sum are equal to zero. In the static equilibrium state, the object always remains at rest so that's why the static equilibrium can be used to determine or understand those objects that can't move and always remain at rest. Simply static means rest so static equilibrium can only achieved by those objects or systems that can't be moved.
Mathematical expression:
As we know in static equilibrium the all forces sum is equal to 0 then it can be written as:
F = 0
F represents the sum of all forces that can be acted on the body or object.
Or the sum of torque is also equal to zero, hence it can be written as:
𝛕 = 0
𝛕 represents the sum of all torques that can be acted on the body or object.
For instance:
The book can be lying on the table or at rest, then the forces that can be acted on the table are maintained or normalized through the gravitational force that can be acted on the book which is lying on the table
The bridge that can be used for traffic is always in a static state, then it can maintain its static equilibrium by balancing the forces and the weight or load that act on the bridge.
Chemical equilibrium:
In chemical reactions, chemical equilibrium can be achieved, when the forward and the reverse reaction rates are the same under the same conditions, and when the concentration of the products and the reactants can't be changed during the reaction then this state can be achieved. Mostly in chemistry, the chemical equilibrium can be used to determine or understand the concentration of reaction but in physics sometimes it can be used.
Mathematical expression:
The rate of forward reaction = the rate of reverse reaction
For instance:
The solution of the salt becomes in the equilibrium or saturation state when the rate of salt dissolution is equal to the rate of precipitation. But if we can provide the temperature to the solution of salt then we can change their equilibrium state also.
When we close the container in which hydrogen iodide solution is present, then this solution can achieve the equilibrium state easily because, in the closed container, we can't change the conditions and can't change the temperature or concentration of the reactant and product amount.
Condition of equilibrium:
Two main conditions are essential for achieving the equilibrium state. If the object and the system can't follow these two main conditions then it can't achieve the equilibrium state. The two conditions for the equilibrium state are given there:
The first condition of equilibrium ( equilibrium of forces)
A second condition of equilibrium ( equilibrium of torque
Details of the first condition of equilibrium are given there:
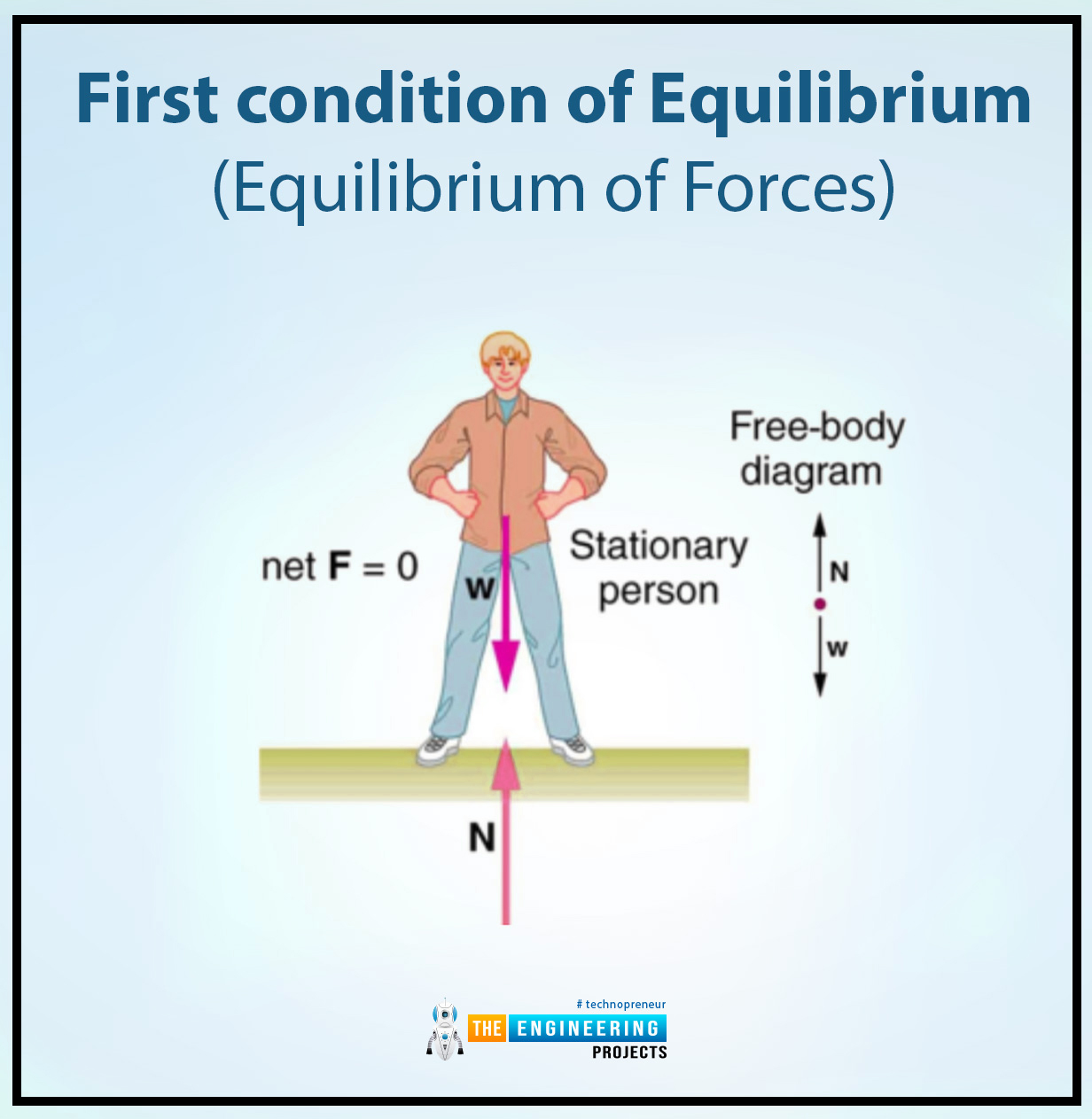
First condition of equilibrium: ( equilibrium of forces)
The first condition of equilibrium is also known or referred to as the equilibrium of forces because in this condition all forces that act on the body or the object must equal to zero. If the system or the object can't follow this condition then it never can achieve the equilibrium state.
Definition:
The first condition of equilibrium or the equilibrium of forces can be defined as:
The sum of all vector forces that can act on the object or any system externally is always equal or must equal to zero. Mathematically it can be written as:
F = 0
This equation proves or shows that the sum of all forces is equal to zero so that is why the object that is at rest or motion has not been accelerated because the object is in a uniform state of motion or the rest.

Mathematical expression:
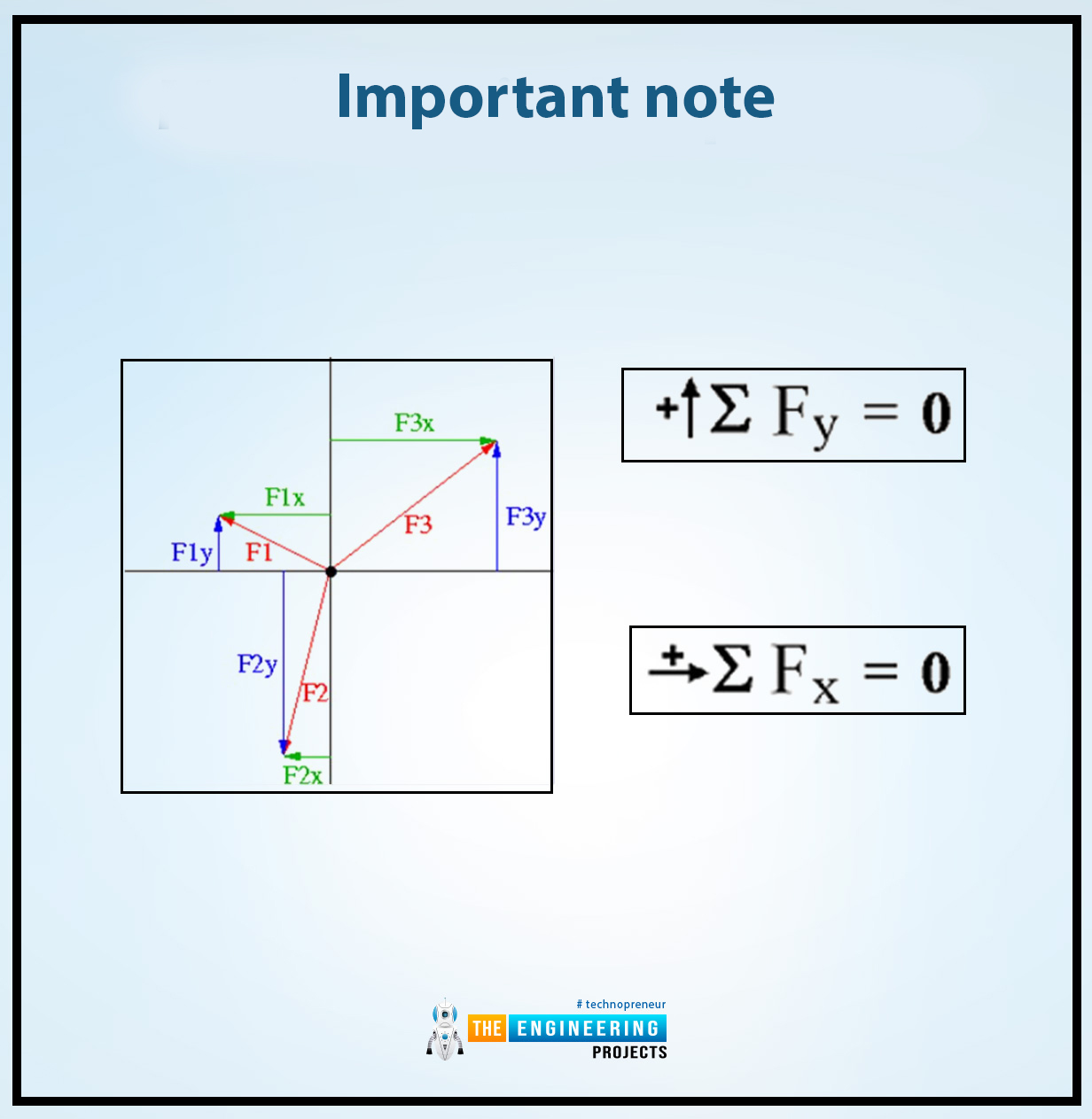
If the system which can follow the first condition of equilibrium to achieve the state of equilibrium can lie in the two dimensions then it can be written as:
Fx = 0
This equation or formula represented the sum of all forces in the x direction.
Fy = 0
This equation or formula represented the sum of all forces in the y direction.
Both equations can be used in the two dimension system. But if we balanced the three-dimensional system then the forces are directed on three axes x, y, and z and it can be written as:
Fx = 0
This equation or formula represented the sum of all forces in the x direction.
Fy = 0
This equation or formula represented the sum of all forces in the y direction.
Fz = 0
This equation or formula represented the sum of all forces in the z-direction.
Important note:
If the forces that can be acted on the object or system are taken in the right direction then these forces are positive.
If the forces that can be acted on the object or system are taken in the left direction then these forces are positive.
If the forces that can be acted on the object or system are taken in the upward direction then these forces are positive.
If the forces that can be acted on the object or system are taken in the downward direction then these forces are positive.
If the forces that can be acted on the object or system are common in plane then these forces are termed as the coplanar.
Significance of the first condition of equilibrium:
All stationary and static systems can be analyzed or understood through the first condition of equilibrium. The branch of mechanics in physics, the concept of equilibrium can be discussed in statics principle in which we can deal with or study the forces that can act on a stationary system or object. The equilibrium of forces is fundamentally used for understanding or analyzing the
Structural analysis
Mechanical analysis or designs
Everyday applications
Everyday applications:
Every day we can use many different objects in which the equilibrium can be seen. In common conditions like hanging the objects and placing different things one by one or balancing them. In hanging or balancing things can be done by the equilibrium so we can also understand the equilibrium interactions in our daily life.
Structural analysis:
In engineering or physics, we can understand the structures of the system through which the balance can be maintained like the bridges, roads, and buildings that can carry the load stabilized due to the equilibrium condition by balancing the all forces which can act upon it.
Ensuring the stability of buildings, bridges, and other structures under various loads.
Mechanical analysis or design:
In the field of mechanics, equilibrium conditions can be followed to design the efficient machine or their designs. In designing the machines the components are chosen that can stand with the forces that can act upon it and maintain them efficiently at the rest or in motion also.
Examples and some problem-solving:
The equilibrium in the static sign can be hung on the wall.
Let us consider the sign that we can hang on the wall with two ropes so they have different angles. The angle that can be made by the ropes during hanging is approximately 30° or 45°. The weight of the sign that can be hanged is 100N. Now we can find or determine the tension that can be produced in ropes for balancing the sign on the wall.
Now let the T1 tension for the first rope which can make an angle of 45° and T2 the tension for the second rope which can make an angle of 55°. For achieving the equilibrium state all forces that can act on the sign in the x and y direction, their sum is must be equal to 0.
The forces that can act in the x direction:
T1 cos (30) = T2 cos (45)
The forces which can act on the y direction:
T1 sin ( 30) + T2 sin ( 45) = 100
Now we can solve both of these equations and write as:
T1 cos (30) = T2 cos (45)
T1 32 = T2 12
And then it can be written as:
T1 = T2 23 12
Then,
T1 = T2 26
T1 = T2 23 ……. (i) equation
Now we can solve the equation in which force can be acted in the direction of y and it can be written as;
T1 sin ( 30) + T2 sin ( 45) = 100
T1 12 + T2 22 = 100
Now we can put the value of T1 in the given equation and write it as:
(T2 23 ) 12 + T2 22 = 100
T2 (23 . 12 + 22 ) =100
Then,
T2 ( 22 3 + 22) =100
T2 ( 2 (1 + 3)23) = 100
T2 = 200 32 (1 + 3)
Then,
T2 = 73. 2 N
Applications of the first condition of equilibrium:
Equilibrium of forces or the first condition of equilibrium can be used in many different fields because it can help to describe the forces or to maintain the system some applications of equilibrium of forces are given there:
Structural engineering
Everyday situations
Mechanical systems
Structural engineering:
In the field of engineering, where bridges buildings, and many other machines can be designed their equilibrium of forces is essentially used because it can ensure that the design or the components we can use have the ability to carry the load to maintain their balance. And can't collapse or be destroyed due to the imbalance of force or weight. Engineers study or examine whether the components that they can use are efficient or attain equilibrium efficiently or not.
Example:
The engineer can design the bridge through which the traffic can be passed, they use the best components and materials that can manage the forces carry the load efficiently, and attain the equilibrium state without deforming or collapsing.
Everyday situations:
Every day we can use many different objects in which the equilibrium can be seen. In common conditions like hanging the objects and placing different things one by one or balancing them. In hanging or balancing things can be done by the equilibrium so we can also understand the equilibrium interactions in our daily life.
Example:
When we hang the pictures or any sign on the wall with ropes then the ropes can manage the tension and all forces that can be acted on them and stabilize them to hang the wall without falling. The all forces which can be acted on the ropes and the sign or picture their sum are always equal to zero. And after neutralizing the forces they can achieve stabilization or equilibrium.
Mechanical system:
In the field of mechanics, equilibrium conditions can be followed to design the efficient machine or their designs. In designing the machines the components are chosen that can stand with the forces that can act upon it and maintain them efficiently at the rest or in motion also. In the mechanical field, engineers choose the components very precisely to maintain the equilibrium state.
Examples:
When engineers make heavy machines or vehicles like cranes then they check or ensure that the forces that can be acted on the crane arm or the load that can be placed on it are capable of bearing it or not. After ensuring these components' ability they can be allowed to use it or made efficient and heavy machinery.
Advanced topic in which first condition equilibrium can be used:
In the modern era of science and technology, the equilibrium of forces can be used in many new fields according to their need. Some new topics in which the equilibrium of forces can be used are given there:
Equilibrium in elastic system
Equilibrium in three-dimension
Equilibrium in the system with friction
Equilibrium in the elastic system:
In the elastic system, the equilibrium can be used because when we stretch the spring it can be restored and maintained by balancing the forces that can be acted on it. Equilibrium is essential in all systems and objects because without equilibrium the system can't work properly.
Equilibrium in three dimensions:
In two dimensions equilibrium can easily attained but now in three dimensions equilibrium must attained by balancing the forces and using the best components in it. For instance, cranes and the tripod or the tables can stand in equilibrium and manage the forces acting upon it in the three dimensions x, y, and z efficiently.
Equilibrium in the system with friction:
In equilibrium problems, friction can play a vital role. Because when the system interacts with the surface it is obvious that friction can be produced so when we calculate the system's net force for their equilibrium the force of friction can also be calculated because sometimes, friction is the restriction in attaining the equilibrium set. For instance, if we place a block on the surface or the plane then if we want to stabilize the block at the right position it is a must to calculate the all forces that can act on the block along with the force of friction.
Practical examples of equilibrium of forces:
Some practical examples in which the equilibrium of forces are commonly used to maintain their work or maintain their output efficiency or control on them are given there:
Robotics
Automotive engineering
Architecture
Building designing
Aerospace engineering
Conclusion:
In the era of modern science and technology, the first condition of equilibrium can play a fundamental role in different fields like physics, mechanics, chemicals, or engineering because it can provide basic information and help to understand all static systems and objects efficiently. By understanding this condition of equilibrium we can achieve the system balanced without producing the error or acceleration. Through their application in many new fields, we can easily understand them because this condition of equilibrium can be used in our daily life situations. The equilibrium of forces is easy to understand because in this the sum of forces is always equal to zero or the forces include the normal force, gravitational force, or maybe the frictional force. But with time it can be more commonly used in the field of science. Equilibrium of forces is the fundamental concept in the field of static or dynamics



