Hi friends, I hope you are all well. In this article, we can discuss the scalar or dot products of the vectors. In previous articles, we have discussed vectors and their addition in the rectangular or cartesian coordinate system in depth. Now we can talk about the scalar product of two vectors, also known as the dot product. Scalar or dot products can play an essential role in solving the operation of vector algebra and also they have various applications in numerous fields like computer sciences, mathematics, engineering, and physics.
By doing the scalar or dot products, two vectors are combined when we can do their product, then they produce the scalar quantity which has both magnitude and direction by a single operation in a very efficient way. Simply the scalar and the dot product are algebraic operations that can be especially used in physics and mathematics. scalar quantity can only provide the magnitude but when we can do the product of two vectors, the result of this product is scalar quantity which provides and describes both magnitude and direction. The angle between the two vectors can also be found through the scalar or dot product. The dot product term can be derived from the word dot operator and it can be used for the product of two vectors but it can also known as a scalar product because it can always give the result as a scalar quantity so that is why it can also be known as scalar product rather than the vector product.
Now we can start our detailed discussion but the dot or the scalar product, their definition, algebraic operations, characteristics, applications, and examples. At the end of this discussion, the reader easily understands vectors, how we can make the scalar product, and their application in numerous fields of science, especially in physics or mathematics.
Definition:
Dot/Scalar products can be defined geometrically or algebraically. But in the modern form, the scalar and the dot product can be defined and rely on the Euclidean space which has the cartesian or rectangular coordinate system. The basic and simple definition of the scalar and the dot product are given there:
“The product of two vectors is a scalar quantity so that's why the product is termed scalar product”.
Mathematical expression:
The mathematic expression which can express the dot or scalar product is given there:
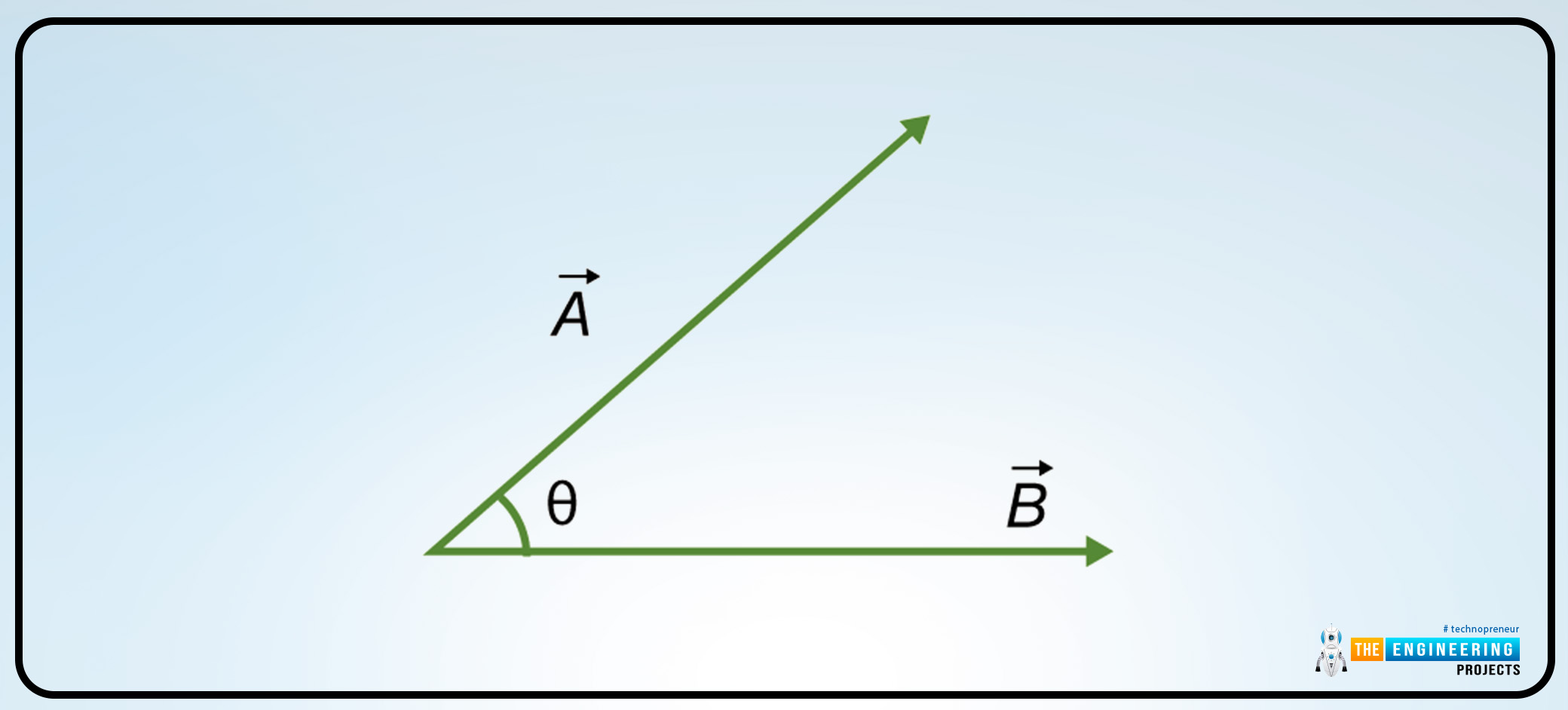
A B = AB cosθ
Where,
A is the magnitude of the vector A.
B is the magnitude of the vector B.
And,
The cosθ is the angle between the two vectors A and the vector B.
Coordinate definition of the scalar product:
The dot product or the scalar product produces a single scalar quantity which can be produced through their mathematical operation. The product of the two vectors based on orthonormal base or in n-dimensional space, their mathematical expression or definition are given there:
A B = A1b1 + A2B2+ ……… + AnBn
There;
A = A1 , A2, ........ , An
B = B1, B2 , ......... , Bn
A B can also be mathematically written as;
A B = i=1naibi
there n represented the dimension of the vector in the Euclidian space or the summation is represented through.
For example, the dot or scalar product of the vector A = ( 5, 4, 4) or vector B = (2, 1, 6) in the three dimensions is calculated as:
A B = A1b1 + A2B2+ ……… + AnBn
By putting the values we can get,
A B = ( 5 2) + ( 4 1) + ( 4 6)
A B = 10 + 4 + 24
A B = 38
moreover, the vectors ( 6, 3, -2 ) themselves can do dot or scalar products which can be written as:
( 6, 3, -2) ( 6, 3, -2) = (6 6) + (3 3) + (-2 -2)
= 36 + 9 + 4
= 49
Another example for the dot or scalar product of the vector A= ( 4,6) and the vector B= ( 2, 8) in the two dimensions can be expressed or calculated as:
( 4, 6) ( 2,8 ) = ( 4 2) + ( 6 8)
= 8 + 48
= 56
The product of the two vectors can also be written in the form of a matrix. The formula that can be used for the matrix product of two vectors can be written as
A B = At. B
There,
At = transpose of the vector A
For instance,
4 3 2 4 9 4 then this matrix has vectors column 1 1 = 1
And the column in this vector is 3 3 = 6
In this way, we can write the vectors in the matrix row or column form and the result is a single entity.
Geometrical definition of the scalar or the dot product:
In geometry, Euclidean vectors can describe both magnitude and direction through the scalar product or from the dot product. The length of the vector represents the magnitude and the direction of these vectors can be represented through the arrow points that are present on the vectors. The scalar and the dot product in geometry can be written as;
A B = A B cosθ
There,
A represented the magnitude of the vector A.
B represented the magnitude of the vector B.
And,
θ represented the angle between the magnitude of the vector A and the vector B.
Orthogonal vectors:
If the vector A and the vector B are orthogonal then the angle between them θ = 90° or also equal to the π2 it can be written as:
A B = cosπ2
hence,
The cosπ2 is equal to 0. It can be written as:
A B = 0
Codirectional:
If the vector A and the vector B are codirectional then the angle between their magnitude is equal to 0. Then,
A B = cos 0
hence,
cos0 = 1 and written as:
A B = A B
Itself vector product:
If the vector A does scalar or the dot product itself then it can be written as:
A A = A2
That can also written as:
A = A . A
This formula can be used to determine the length of the Euclidean vector.
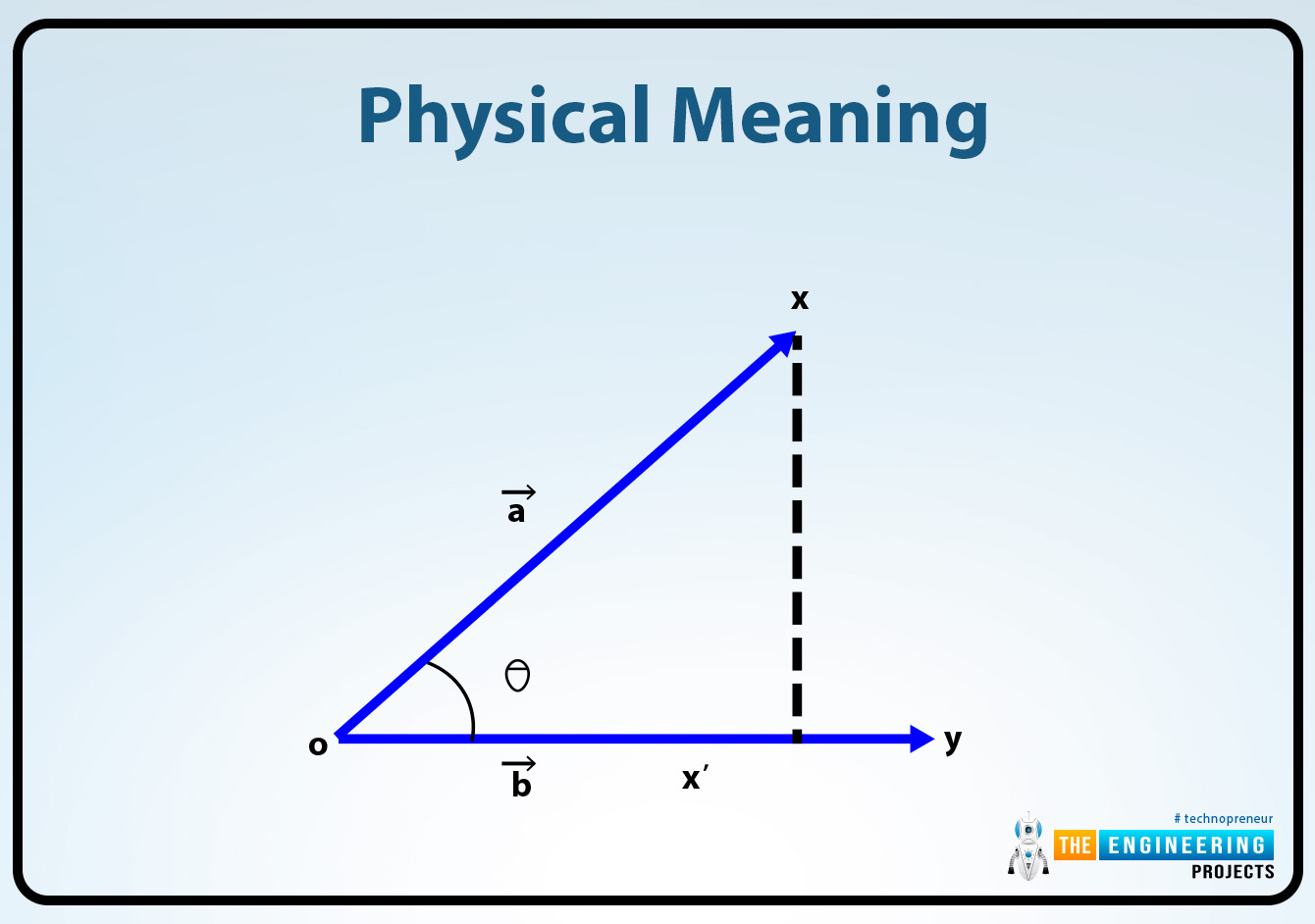
Physical meaning:
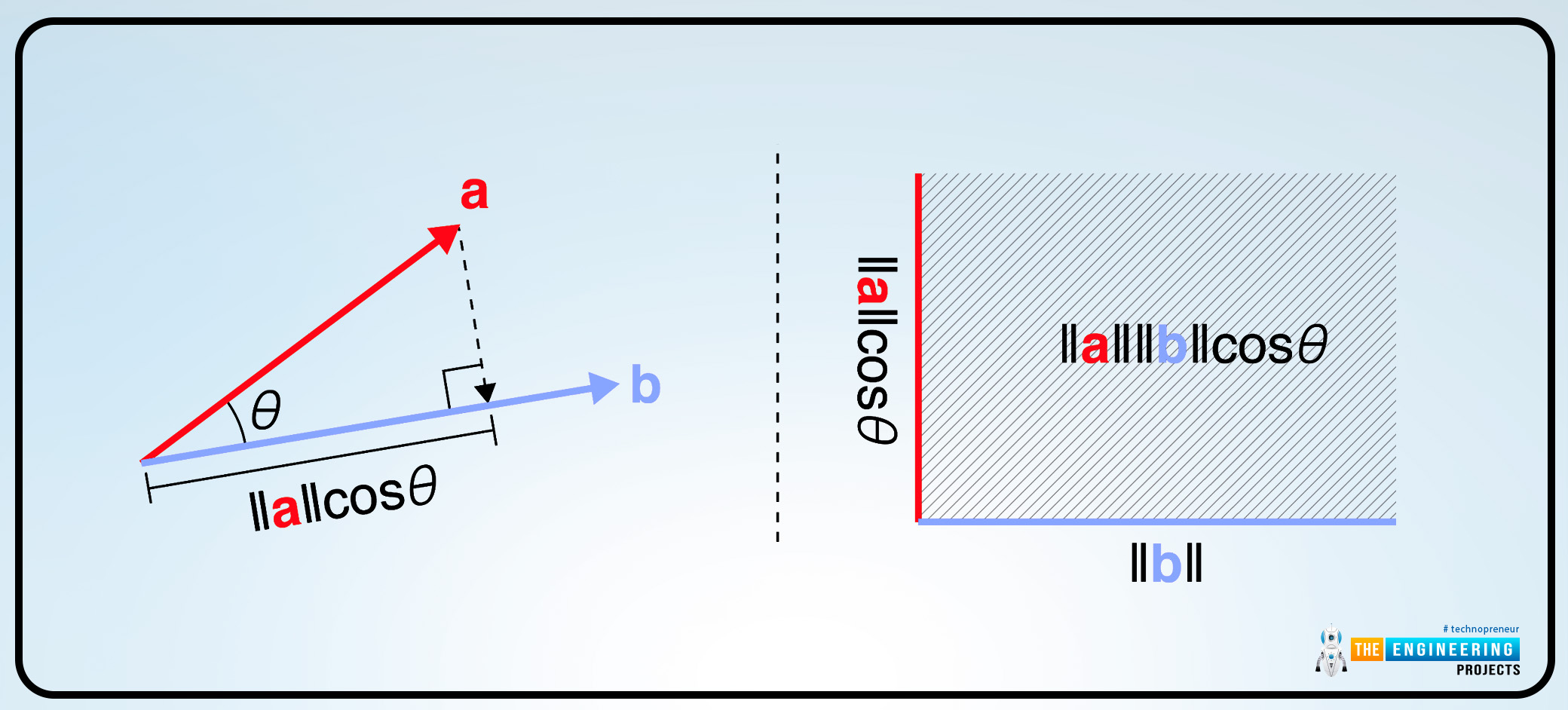
The simple physical meaning of the scalar or dot product is that the product of the dot or scalar product is equal to the magnitude of the one vector and the other is equal to the component of the second vector which is placed in the direction of the first vector.
Mathematically it can be expressed as:
A B = A ( projection of the vector B on the A).
A B = B (the component of vector B magnitude along with the vector A )
Then it can also be written as:
A B = A ( B cosθ )
Then for the vector B we can write as:
B . A = B ( projection of the vector A on the vector B)
B . A = B ( the component of vector A magnitude along with the vector B).
Then it can also be written as:
B . A = B ( A cosθ)
First property and the scalar product projection:
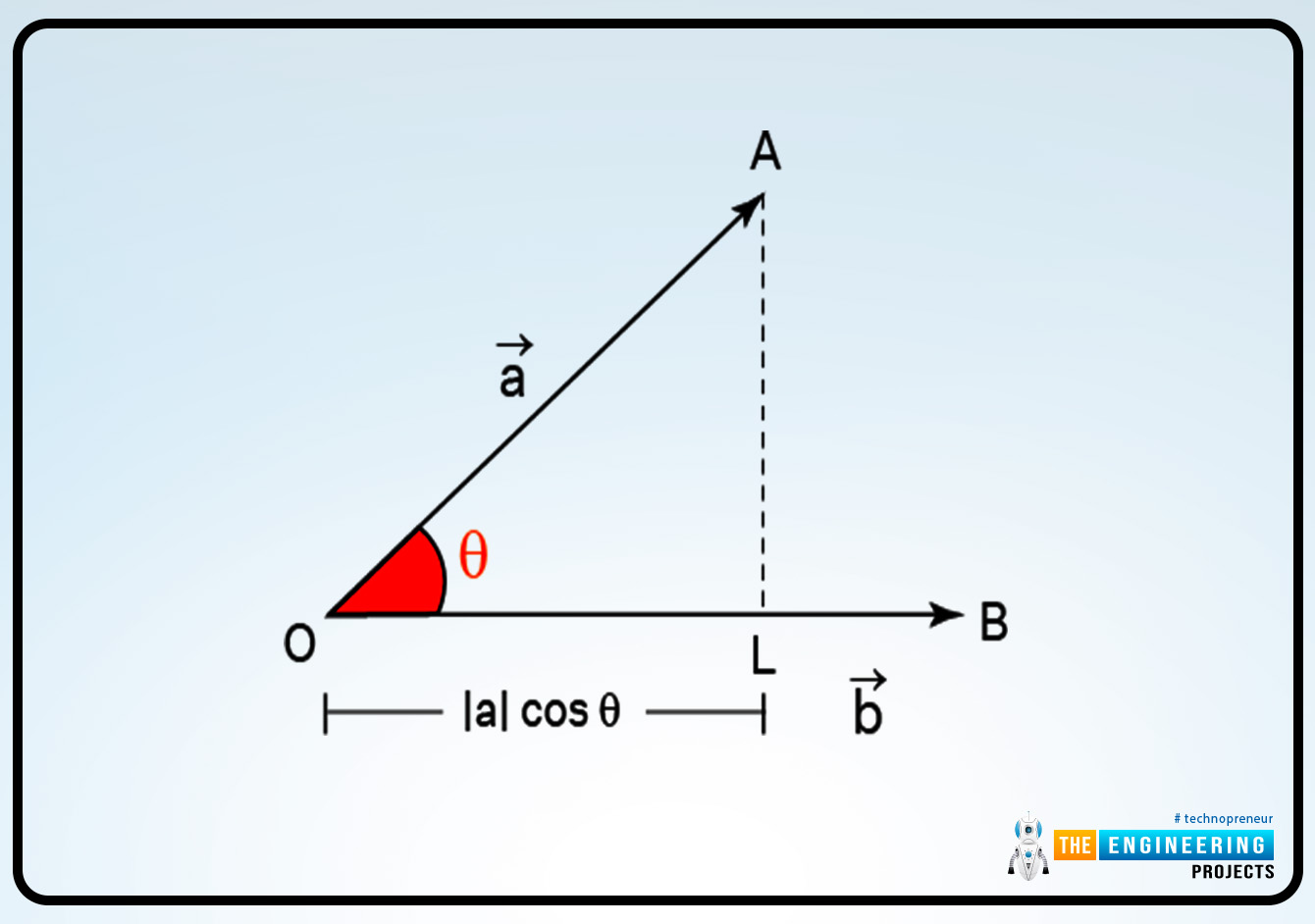
The other physical meaning or the projection of vectors with their first property can discussed in detail. the projection of vector A in the direction of the vector B can also be written as:
Ab = A cosθ
The θ is the angle between the two vectors A and the vector B.
Geometric definition:
This product can also be written according to the definition of geometrical dot product then it can be written as:
Ab = A B
There,
B = BB
so, geometrically we can write the projection of A on the vector B as:
A B = Ab B
For the vector B, it can be written as:
A B = BaA
Distributive law:
The dot product can also prove the distributive law, the distributive law is written as:
A ( B + C) = A B + A C
This law can be satisfied by the dot product because the scaling of any variable is homogenous. For example, if we can take the scalar B then it can be written as:
( BB) A = B ( B A)
Also written as,
( BB) A = B ( B A )
The dot product of the B B is always positive it never be negative but it may also equal to zero.
Interchangeability of the definitions:
Determine the standard basic vectors E1, E2, E3, ……., En. So we can also write this as:
A = A1, A2, A3, ...... , An also equal to iAiEi
B = B1, B2, B3, ...... , Bn also equal to iBiEi
This formula Ei can represent the unit length of the vectors. Also represented that the length of the unit is at the right angle.
The normal unit length of the vector is equal to 1 and written as:
Ei Ei = 1
But when the length of unit vectors is at the right angle then it can be written as:
Ei Ej = 0
there, i ≠ j.
Basically, we can write the all formulas as:
Ei Ej = δij
there, Ei or the Ej represented the orthogonal vectors unit length and the δij represented the Korenckar delta.
Geometrical definition for the vector A and the vector Ei:
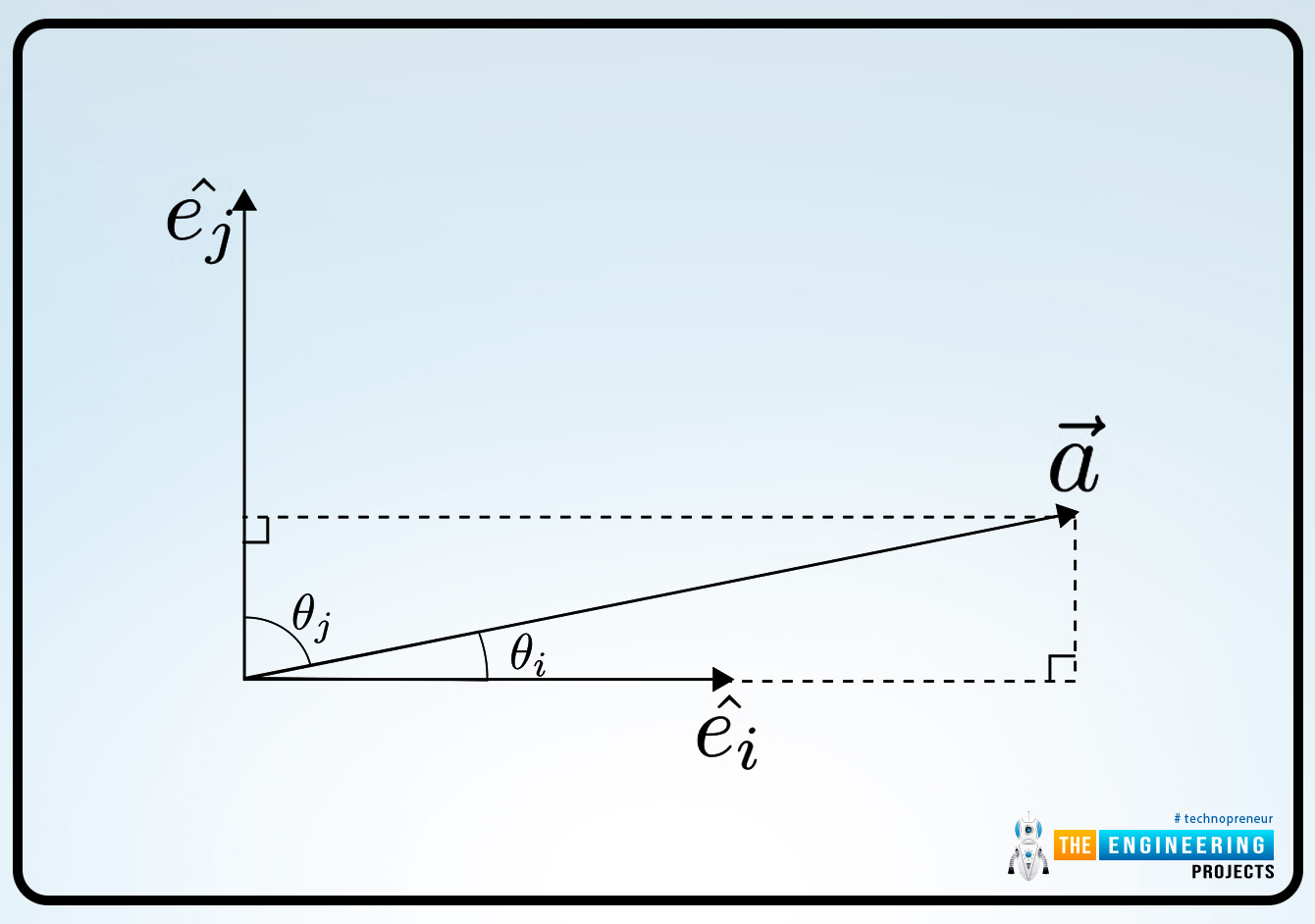
According to the geometrical definition of the dot or scalar product, we can write the given expression for any different type of vector A and the vector Ei. the mathematical expression is written as:
A Ei = A Ei cosθi
or,
Ai = A cosθi
Distributive law:
Now apply the distributive law on the given formula which is according to the geometrical scalar product or the dot product. The distributive version of this formula is given there:
A B = A i BiEi
It can also equal to,
= i Bi( A Ei)
= i Bi Ai
= i AiBi
Now it interchangeability of all definitions can be proved. It can be shown that all definitions of formulas are equal to each other.
Geometric interruptions:
In the dot product or the scalar product the geometrical interpretations are essential because they can relate the magnitude of the vectors through the dot product and the dot product can also give the angle between the vectors which are cosine. The main geometrical interruptions are given there:
Projection
Orthonogolity
Parallel vectors
Anti-parallel vectors
Their details are given there:
Projection:
By the dot or the scalar products, we can measure the direction and the projection of the vector how much the vector lies on the other vector in the projected direction. For instance, A B through we can measure the projection of vector A on the vector B in a very efficient way.
Orthogonality:
When the two vectors are perpendicular to each other, then their dot or the cross product is zero because the angle θ is equal to 90 degrees and the cos90 degree is equal to zero. So if the dot or cross product of the vector quantity is zero then it means that the vectors are orthogonal.
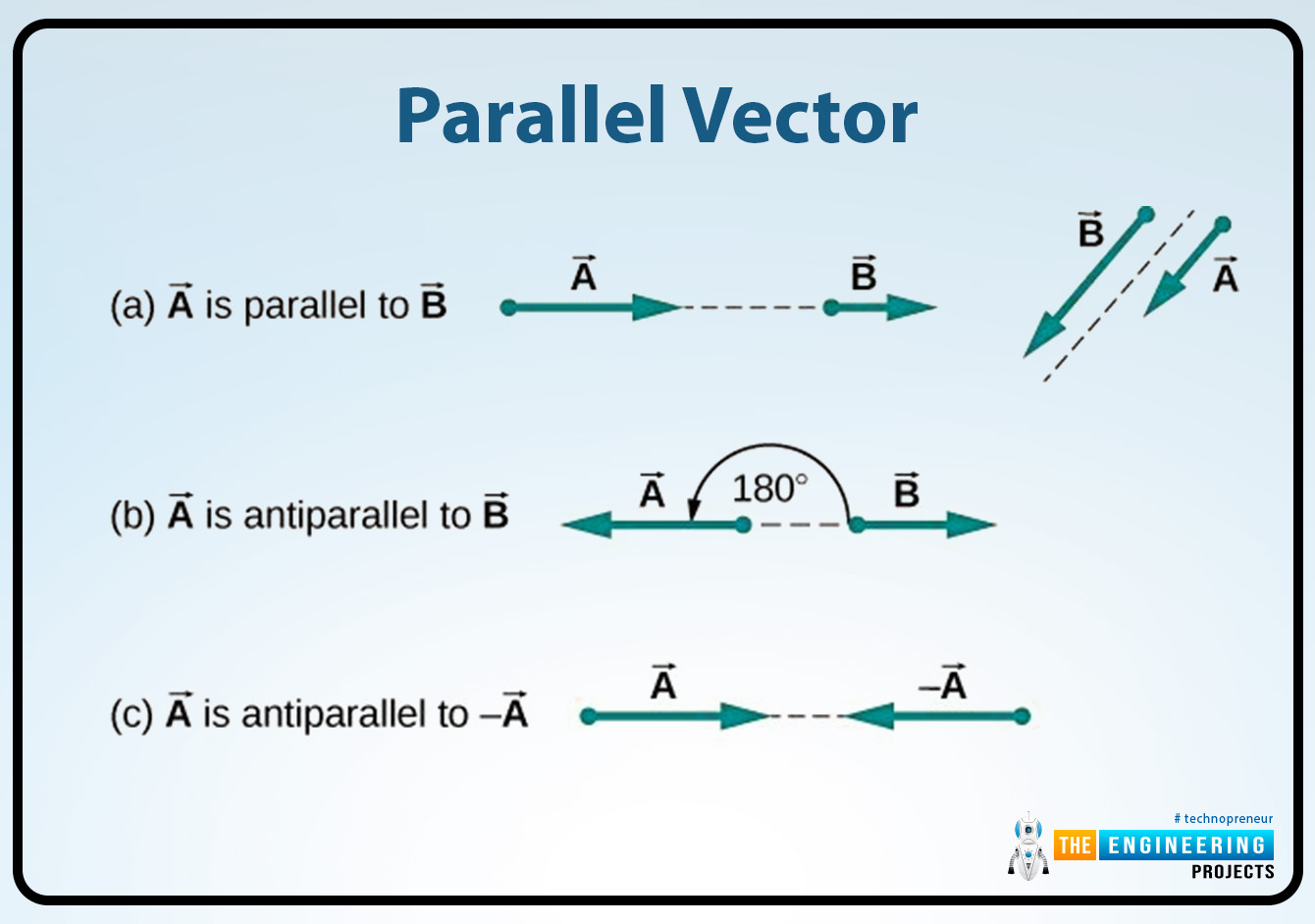
Parallel vectors:
In the dot or the cross product, if the vectors are parallel then the angle θ is equal to 0 degrees then the cos θ = 1, which means that the dot or cross product reached their maximum positive or negative magnitude.
Anti-parallel vectors:
In the dot or the cross product, if the vectors are anti-parallel then the angle θ is equal to 180 degrees then the cos θ = 1, which means that the dot or cross product reached their maximum positive or negative magnitude.
Characteristics and the properties of the scalar or the dot product:
The main properties and the characteristics of the scalar and the dot product which can help to understand the dot or scalar product are given there. By understanding pr follow the given properties we can easily use this dot product in different fields of science and physics. The characteristics in detail are given there:
Distributive property
Parallel vectors
Anti parallel vectors
Self scalar products
Scalar multiplications
Commutative property
Perpendicular vectors
Magnitude
Product rule
Orthogonal
Scalar product in the term of rectangular component.
Zero vector
Distributive property:
The distributive property of the dot or the scalar product can be strewed upon the vector addition. The basic and general expression for the distributive property for the dot or cross product is given there:
A ( B + C ) = A B + A C
Parallel vector:
The scalar or dot product of the two vectors is equal to their positive magnitude when the vectors which are used in the dot or scalar product are parallel to each other and their angle θ is equal to 0 degrees, it can be written as:
θ = 0°
The mathematical expression for parallel; vector can be written as:
A B = AB cos 0°
and, cos 0° equal to 1 and written as:
A B = AB (1)
A B = Ab
hence, it can be shown in the above equation that the product of two vectors is equal to their magnitudes. It can also be the positive maximum value of the scalar or the dot product.
Anti-parallel vectors:
The scalar or dot product of the two vectors is equal to their negative magnitude when the vectors which are used in the dot or scalar product are anti-parallel to each other and their angle θ is equal to 180 degrees, it can be written as:
θ = 180°
The mathematical expression for an anti-parallel vector can be written as:
A B = AB cos 180°
and, cos 0° equal to 1 and written as:
A B = AB (-1)
A B = -Ab
hence, it can be shown in the above equation that the product of two vectors is equal to their magnitudes. It can also be the negative maximum value of the scalar or the dot product.
Scalar multiplication:
The dot product or the scalar product can directly affect the scaling of the vector. Through this property of the dot or cross product, we can observe this effect efficiently. The equation that can be used for the scalar multiplication property is given there:
(c1 A ) ( c2 B ) = c1c2 ( A B)
There c represented the scalar quantity.
Self scalar product:
When the vector can do their self-product then the result is always equal to the square of their magnitudes.
The basic and the general equation is written below:
A B = AA cos 0°
A B = AA (1)
A B = A2
It can be shown in the given equation that the self-product was always equal to the square of their magnitudes.
Self product of unit vectors:
The self-product of the unit vectors is always equal to the 1. Their clarification through mathematical expression is given there:
i i = (1) (1) cos 0°
i i = (1) (1) (1)
i i = 1
So,
j j = 1
k k = 1
Hence,
i i = j j = k k
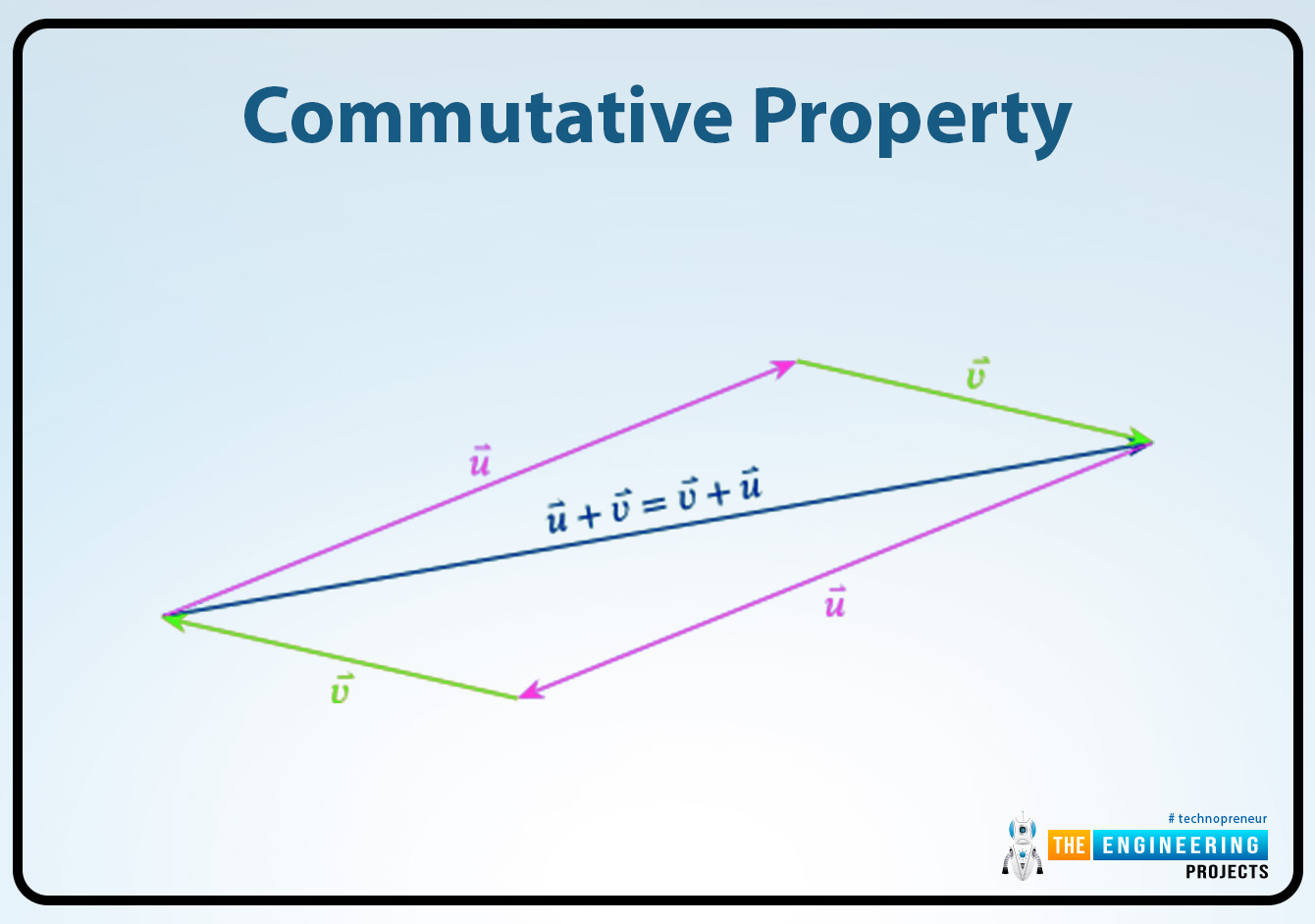
Commutative property:
The scalar or the dot product of two vectors A and B are always commutative. Their mathematical justification is given there:
A B = AB cos θ …….. (i) equation
there, A represented the vector
B also represented the other vector
And θ represented the angle between the vectors A and B.
then,
B A = BA cos θ ………. (ii) equation
Then, by comparing the equation i and the equation ii,
A B = B A
Hence proved that the dot or scalar product is always commutative.
Zero vector:
In the product of two vectors if one vector A = 0 then the other vector B = 4 but their product is always equal to zero. Their mathematical expression is written there as:
= A B
= (0) (4)
Then,
A B = 0
Orthogonal:
If the two vector scalar or dot products are equal to zero then it can't be orthogonal but if the two vectors are non-zero variables it can be orthogonal.
Product rule:
In the scalar or the dot product, the values are different or variable and their deviation can be represented through the sign which is known as the prime ′. Their mathematical expressions are given there:
( A B) ′ = A′ B + A B′
Scalar products in terms of rectangular components:
Determine the two vectors, the vector A and the B in the Euclidean space in the three-dimensional cartesian coordinate system. Their derivation is given there:
Let,
A = Axi + Ayj + Azk
B = Bxi + Byj + Bzk
then, we can perform their product with their unit vectors and it can be written as:
A B = (Axi + Ayj + Azk) (Bxi +B yj + Bzk)
After this, we can multiply the all components with each other and it can be written as:
A B = AxBx ( i i ) + AxBy ( i j) + AxBz ( i k) + AyBx ( ji )
AyBy ( j j ) + AyBz ( jk ) + AzBx ( ki) + Az By ( k j) + Az Bz( k k)
Now, by putting the values of the unit vectors then we get,
A B = AxBx (1 ) + AxBy ( 0 ) + AxBz ( 0 ) + AyBx (0 )
AyBy (1 ) + AyBz ( 0 ) + AzBx ( 0 ) + Az By (0) + Az Bz(1)
Then,
A B = AxBx + AyBy + Az Bz ……… (i) equation
We know that ;
A B = AB cos θ ………… (ii) equation
Then put equation (ii) in equation (i) and we get,
AB cos θ = AxBx + AyBy + Az Bz
Or it can also be written as;
cos θ = AxBx + AyBy + Az BzAB
Or,
θ = cos-1AxBx + AyBy + Az BzAB
This formula or the equation can be used to find the angle θ between the vector A and the vector B.
Applications of scalar or dot product:
Scalar or dot products can play a very essential and fundamental role in different fields of modern science or physics, computer graphics, engineering, or data analysis. The details of these applications are given below:
Data analysis or machine learning
Mathematics
Physics
Engineering
Computer graphics
Data analysis or machine learning:
Dot or scalar products can be used in data analysis or machine learning in a very efficient way their applications in this field mostly occur in the given fields area which are;
Natural languaging processing
Principal component analysis
Neural networks
Their description is given below:
Natural languaging processing:
The differences and the similarities that may be present in the natural languaging processor ( NLP) can be detected through the scalar and the dot product because the words can be represented in the form of vectors in NLP. and it can also help to do many numerous tasks like the machine translation, data analysis and the document clustering in a very efficient way.
Principal component analysis:
Principal component analysis which can also be denoted as PCA, to determine and find the principal components that are present in the data can be detected by using the dot or cross-product method. Because it can simplify the most complex data or analyze them in a very efficient way. So that's why cross or dot products can be widely used in this field.
Neural networks:
For the sum of the neurons, we can use the dot or the scalar product. Because of all the neurons, the input vector calculation can always be done through the dot or the cross product, and by the activation the output can be produced.
Mathematics:
In mathematics, the dot and cross product can be used commonly because geometry and the algebraic operation can be solved easily or efficiently through the dot and the cross product. The main fields of math in which the dot and cross product can be used are given there:
Cosine similarity
Orthogonality
Projection
Vector spaces
Physics:
In physics to simplify the complex quantities and products dots or scalar products can be used. The main application fields are given there:
Molecular dynamics
Work done
Electromagnetic theory
Engineering:
In engineering, algebraic operations can be simplified efficiently through the dot or scalar product. But the main areas of this field where mainly dot and scalar products can be used are given there:
Robotics
Signal processing
Structural processing
Computer Graphics:
Like other fields of science, the dot and the scalar product can also be used in computer graphics because through using the dot or scalar product we can efficiently understand or solve the complex codes of words that can be represented in the form of vectors.
Vector projection
Lighting calculations
Shading models
Calculations and some examples:
Work done:
Work is the scalar quantity but it can be a product of two vector quantities through the dot or scalar product. The product of force and displacement produced the scalar product work. Which can be written as:
W = F A
There,
F represented the force.
A represented the displacement.
Calculation:
Consider the force F is ( 4, 5) and the displacement of the object is ( 2, 8 )
Then their product can be written as:
W = F A
By putting the values we can get,
W = ( 4 5) ( 2 8)
W = (20) (16)
W = 36 J
The work that can be done by the body is equal to the 36 J.
Magnetic flux:
The magnetic flux is the product of the two vectors which are magnetic field strength and the vector area which can be expressed as:
Øb = B A
Power :
Power( scalar product ) is the product of two scalar quantity which are force and velocity which are expressed as:
P = F v
Electric flux:
Flux is the scalar quantity and it is the product of the two vector quantities which are electric intensity or the vector area. it can be written as:
Øe = E A