
Hello friends, I hope you are all good. In our previous lecture, we discussed the SI Base Units in detail and today, we are going to discuss the units derived from these base units. In 1960, the International Committee conference was held and they presented the measurement units that are used to measure all quantities worldwide.SI units are used to make accurate and precise measurements.
SI units are the set of seven basic units called base units and all other units are derived from these base units and called derived units. A set of seven base units is used to measure the physical quantities but derived units are used to measure the complex quantities other than physical quantities. SI units play an essential role in modern technology and sciences.

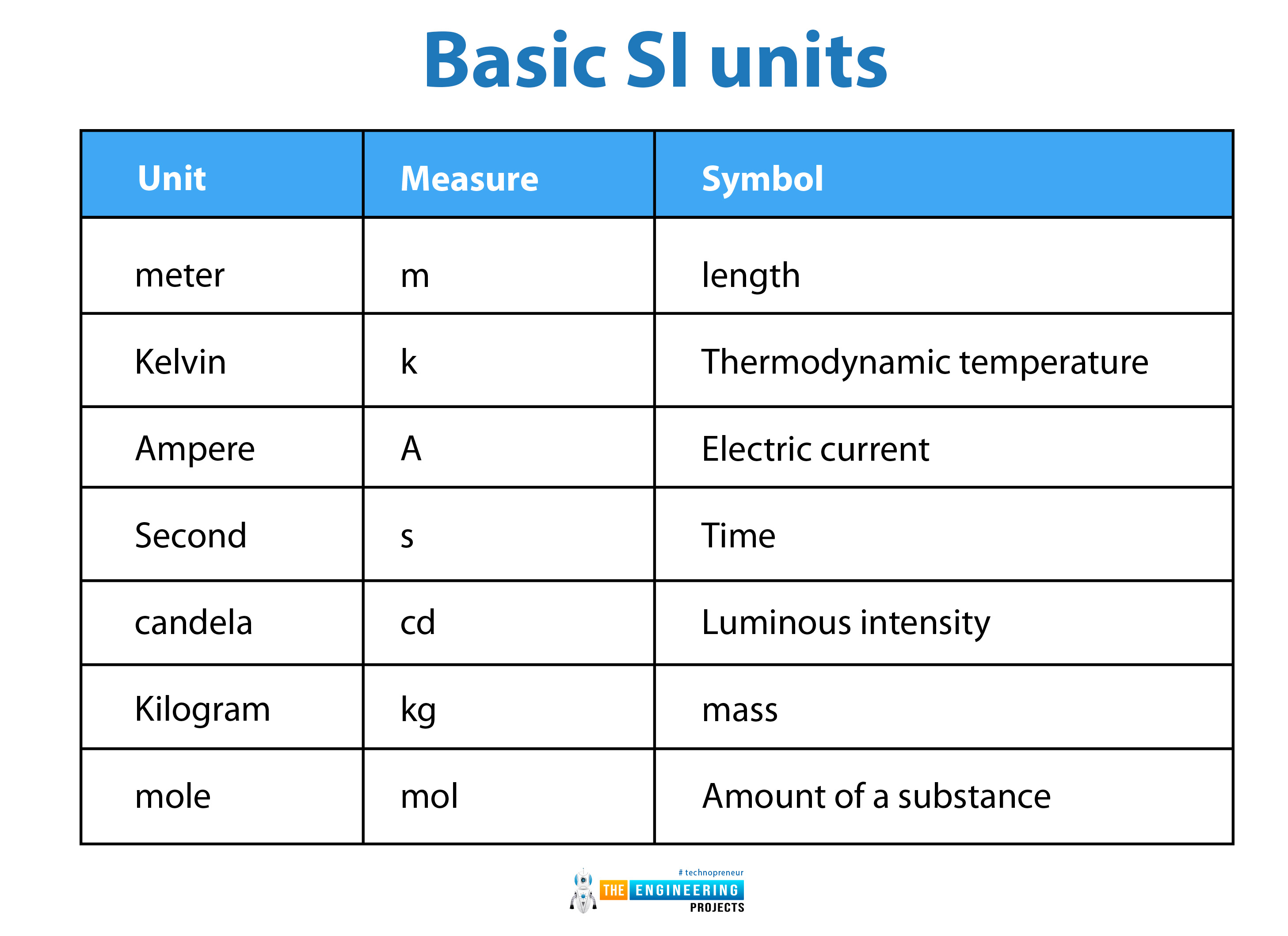
Basic SI units:
The basic SI units from which the other units are derived are given below:
Units |
Symbol |
Measure |
meter |
m |
length |
Kelvin |
k |
Thermodynamic temperature |
Ampere |
A |
Electric current |
Second |
s |
Time |
candela |
cd |
Luminous intensity |
Kilogram |
kg |
mass |
mole |
mol |
Amount of a substance |
These units are the building blocks of all others known as derived units. Derived units are the combination of these base units in the form of an algebraic combination.
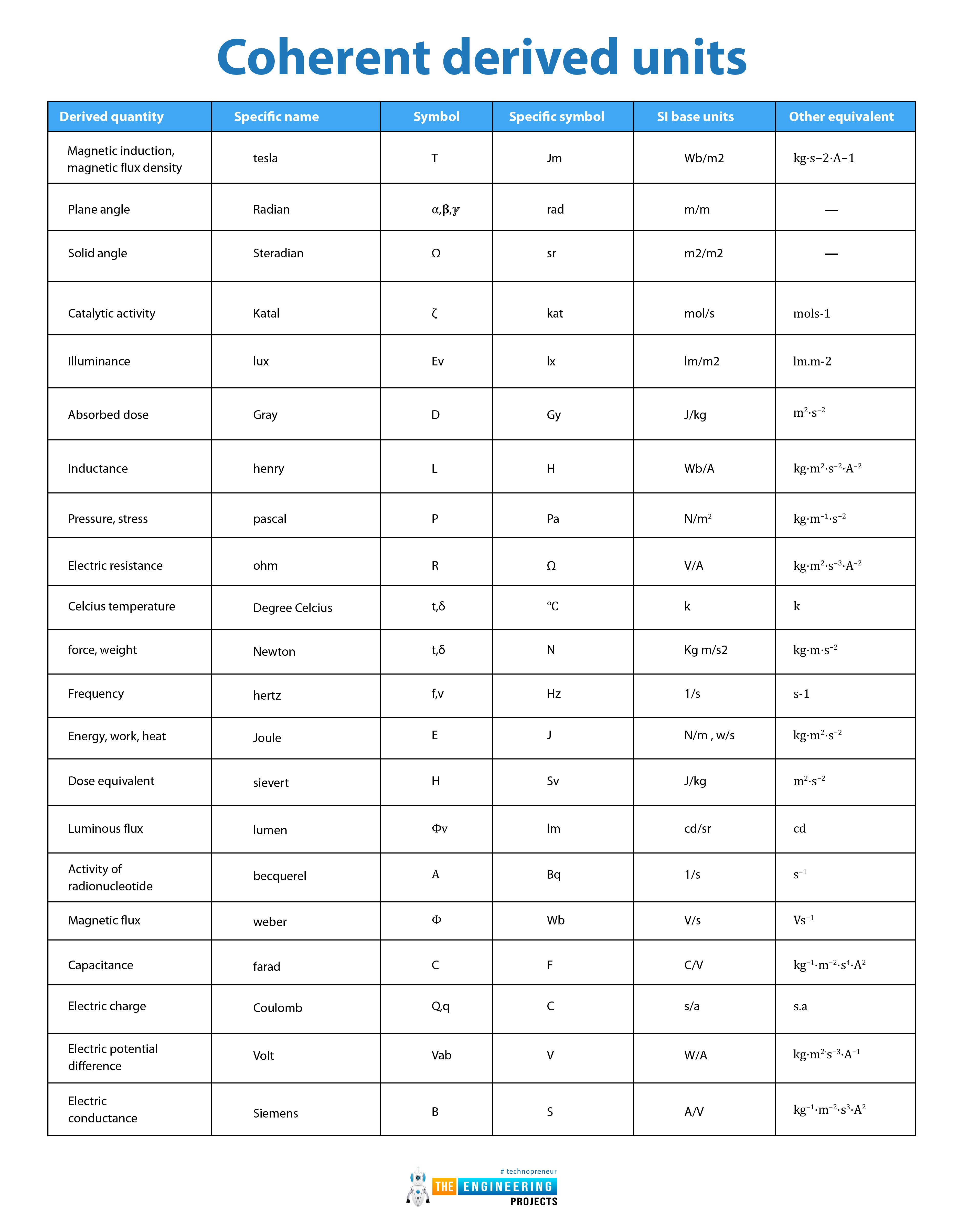
Coherent derived units:
SI-derived units which are also known as coherent-derived units are derived from base units which can be expressed in ratio, product, or exponential form. Some derived units have dimensions but some do not because their demission cancels through their ratio or product.
Derived units are used to measure the complex quantity. Derived and coherent derived units have specific names, symbols, units, and dimensions. All derived units have dimensions except steradian or radian. 22 derived units, their names, symbols, and dimensions are given below:
Derived quantity |
Specific name |
symbol |
Specific symbol |
SI base units |
Other equivalent units |
Magnetic induction, magnetic flux density |
tesla |
T |
Jm |
Wb/m2 |
kg⋅s−2⋅A−1 |
Plane angle |
Radian |
α,𝛃,ℽ |
rad |
m/m |
— |
Solid angle |
Steradian |
Ω |
sr |
m2/m2 |
— |
Catalytic activity |
Katal |
ζ |
kat |
mol/s |
mols-1 |
Illuminance |
lux |
Ev |
lx |
lm/m2 |
lm.m-2 |
Absorbed dose |
Gray |
D |
Gy |
J/kg |
m2⋅s−2 |
Inductance |
henry |
L |
H |
Wb/A |
kg⋅m2⋅s−2⋅A−2 |
Pressure, stress |
pascal |
р |
Pa |
N/m2 |
kg⋅m−1⋅s−2 |
Electric resistance |
ohm |
R |
Ω |
V/A |
kg⋅m2⋅s−3⋅A−2 |
Celcius temperature |
Degree Celcius |
t,δ |
℃ |
k |
k |
force, weight |
Newton |
F |
N |
Kg m/s2 |
kg⋅m⋅s−2 |
Frequency |
hertz |
f,v |
Hz |
1/s |
s-1 |
Energy, work, heat |
Joule |
E |
J |
N/m , w/s |
kg⋅m2⋅s−2 |
Dose equivalent |
sievert |
H |
Sv |
J/kg |
m2⋅s−2 |
Luminous flux |
lumen |
Փv |
lm |
cd/sr |
cd |
Activity of radionucleotide |
becquerel |
A |
Bq |
1/s |
s−1 |
Magnetic flux |
weber |
Փ |
Wb |
V/s |
Vs−1 |
Capacitance |
farad |
C |
F |
C/V |
kg−1⋅m−2⋅s4⋅A2 |
Electric charge |
Coulomb |
Q,q |
C |
s/a |
s.a |
Electric potential difference |
Volt |
Vab |
V |
W/A |
kg⋅m2⋅s−3⋅A−1 |
Electric conductance |
Siemens |
B |
S |
A/V |
kg−1⋅m−2⋅s3⋅A2 |
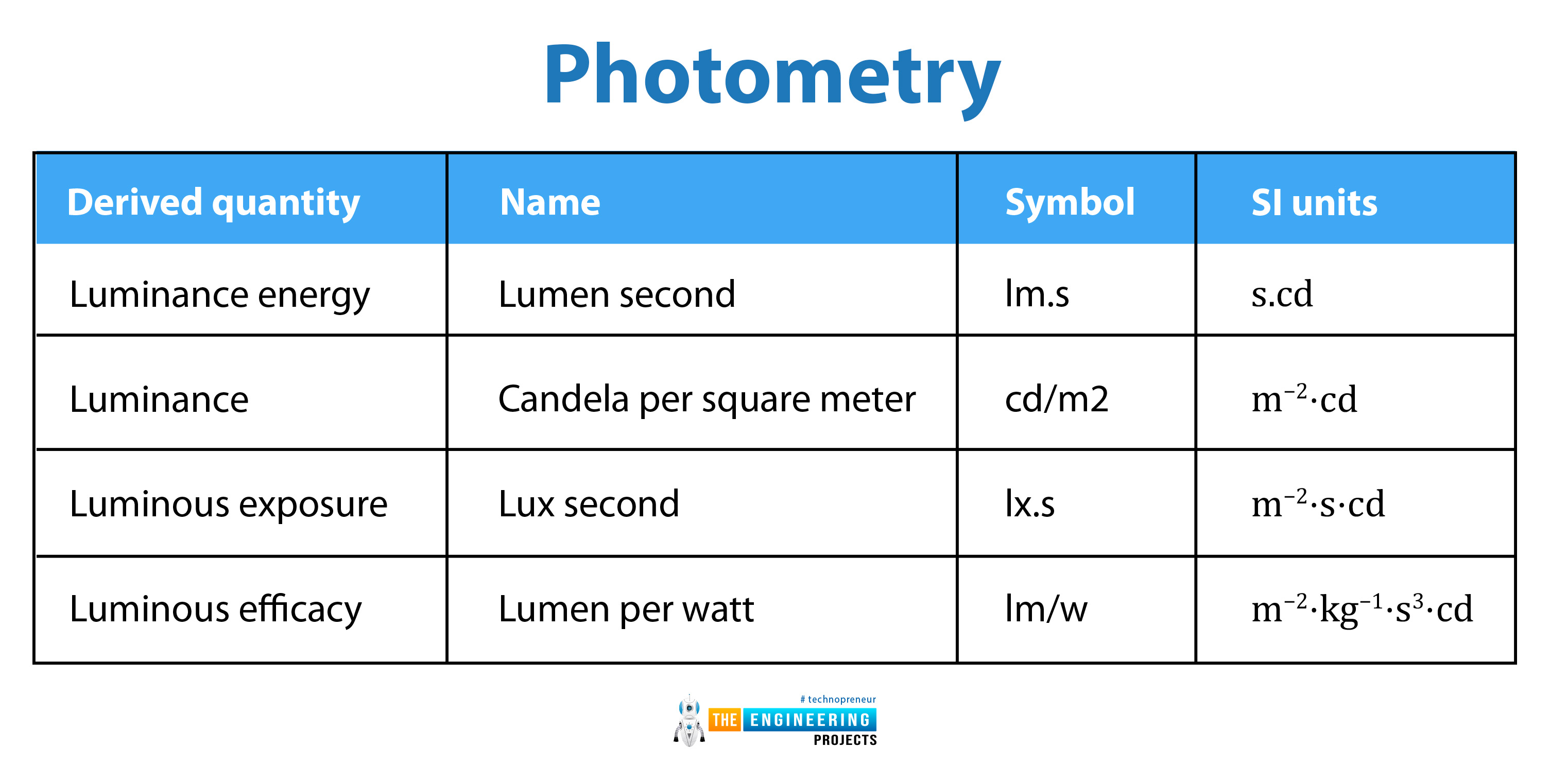
Applications of SI units in different fields:
SI units are used in different fields in chemistry, kinematics, thermodynamics, photometry, kinematics, electromagnetism, or in mechanics. The details are given below:
Photometry:
Derived quantity |
Name |
Symbol |
SI units |
Luminance energy |
Lumen second |
lm.s |
s.cd |
Luminance |
Candela per square meter |
cd/m2 |
m−2⋅cd |
Luminous exposure |
Lux second |
lx.s |
m−2⋅s⋅cd |
Luminous efficacy |
Lumen per watt |
lm/w |
m−2⋅kg−1⋅s3⋅cd |
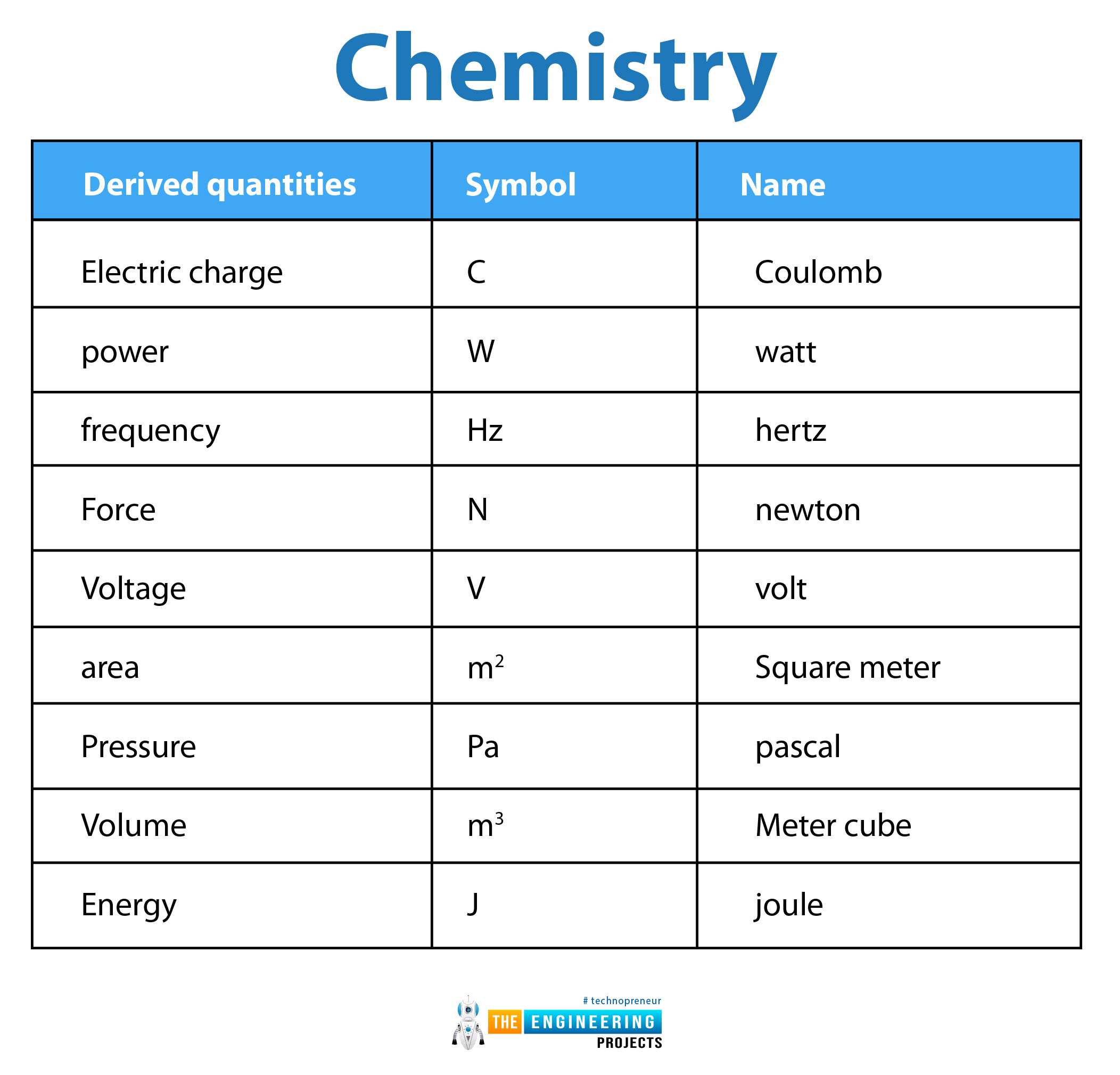
Chemistry:
Derived quantities |
Symbol |
Name |
Electric charge |
C |
Coulomb |
power |
W |
watt |
frequency |
Hz |
hertz |
Force |
N |
newton |
Voltage |
V |
volt |
area |
m2 |
Square meter |
Pressure |
Pa |
pascal |
Volume |
m3 |
Meter cube |
Energy |
J |
joule |
Kinematics:
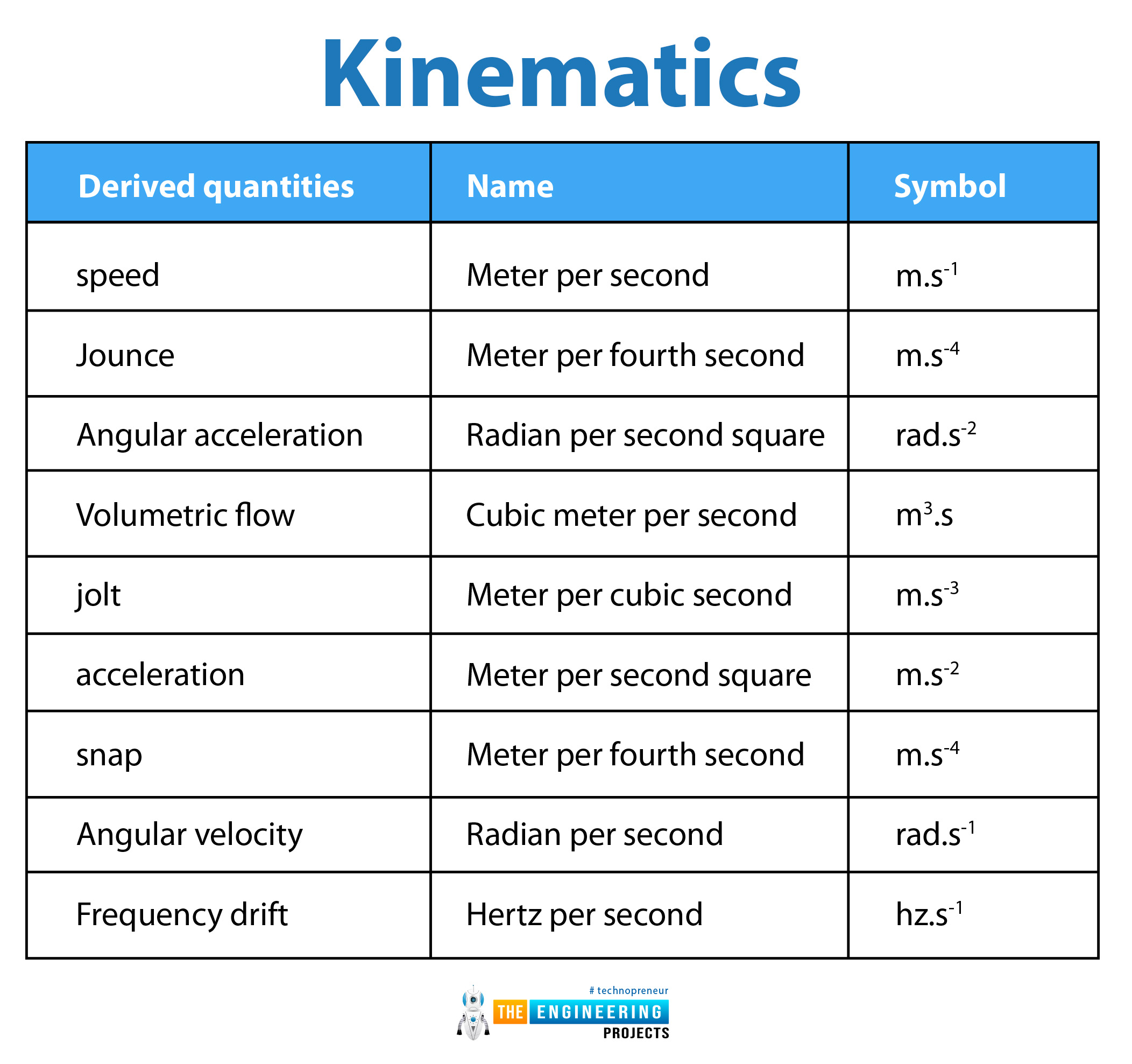
Derived quantities |
Names |
Symbol |
speed |
Meter per second |
m.s-1 |
Jounce |
Meter per fourth second |
m.s-4 |
Angular acceleration |
Radian per second square |
rad.s-2 |
Volumetric flow |
Cubic meter per second |
m3.s |
jolt |
Meter per cubic second |
m.s-3 |
acceleration |
Meter per second square |
m.s-2 |
snap |
Meter per fourth second |
m.s-4 |
Angular velocity |
Radian per second |
rad.s-1 |
Frequency drift |
Hertz per second |
hz.s-1 |
Thermodynamics:

Derived quantities |
Names |
Symbols |
Thermal expansion |
Per kelvin |
k-1 |
Specific entropy |
Joule per kg per kelvin |
J.kg-1.k-1 |
Thermal resistance |
Kelvin per watt |
k.w-1 |
Heat capacity |
Jolue per kelvin |
J.k-1 |
Temperature gradient |
Kelvin per meter |
k.m-1 |
Thermal resistance |
Kelvin per watt |
k. w-1 |
Importance of derived units in physics:
Derived units play a very vital role in physics and many other fields for accurate and precise measurement and also help to understand the physical phenomena. The building blocks of SI units are seven basic units by combining them the all other units derived. Derived units play an essential role in modern science and technology to measure stable and precise measurements.
The importance of derived units in physics is given below:
Standardization and consistency
Efficiency in scientific computation
Practical applications
Simplification of complex quantities
Enhanced power solving
Facilitation of understanding and communication
Interdisciplinary relevance
Details of the importance of derived units are given below:
Efficiency in scientific computations:
The use of derived units enhances computational efficacy in physics. Calculations involving derived units are often more straightforward than those using only base units. For instance, the
Unit watt for power simplifies calculation ]s involving energy and time, eliminating the need for repeated conversions from base units. This efficacy is particularly important in complex calculations, simulations, and models, where reducing the number of steps can significantly impact the accuracy and speed of results.
Interdisciplinary relevance:
Derived units are not confined to physics alone but are used across various scientific disciplines, fostering interdisciplinary research and applications. For instance, the coulomb, a unit of electric charge, is crucial in both physics and chemistry. The use of common derived units across different fields facilitates collaboration and integration of knowledge, leading to achievements in areas such as materials science, biophysics, and environmental science. This interdisciplinary relevance underscores the versatility and universality of derived units in scientific inquiry.
Standardization and consistency:
One of the foremost reasons derived units are vital in their role in standardizing measurement globally. The SI system, established and maintained by the International Bureau of weights and Measures (BIPM), ensures that measurements are consistent and universally accepted. Derived units such as newton(N) for force, the joule (J )for energy, and the watt(W) for power, are constructed from base units like the kilogram(kg), meter(m), and second(s). This standardization is crucial for scientific communication, allowing researchers from different countries and disciplines to compare results and collaborate effectively on confusion or the need for conversion factors.
Practical Applications:
In practical and industrial contexts, derived units are designed to be more user-friendly for real-world measurements. For example, the hertz(Hz) is used to measure frequency, providing a more practical and comprehensible unit than cycles per second. Similarly. The use of derived units like the lumen(lm) for luminous flix or the sievert (Sv) for radiations enables more precise and accessible measurement and regulation in various industries, including healthcare, engineering, and environmental monitoring.
Facilitation of understanding and communication:
Derived units provide a clearer and more intuitive understanding of physical phenomena. For example, energy is measured in joules, which convey specific physical meaning, more straightforwardly than its base unit equivalent. This clarity extends to educational settings, where students can grasp complex concepts more easily when they are expressed in familiar derived units. additionally, using standardized derived units in scientific literature and presentations ensures that findings are communicated effectively, fostering a shared understanding among researchers.
Simplification of complex quantities:
Many physical quantities are inherently complex and can't be conveniently expressed using only base units. Derived units simplify these expressions, making them more manageable and intuitive. For instance, pressure is commonly expressed in pascals(Pa) rather than its base unit form of kg/ms-2. This simplification is not merely a matter of convenience but also aids in understanding and interpreting physical concepts more readily. It allows scientists and engineers to work more efficiently, reducing the potential for error and misinterpretation.
Enhanced problem-solving:
Derived units play a crucial role in problem-solving by aiding in dimensional analysis, which involves checking the consistency of equations. Dimensional analysis ensures that equations are dimensionally consistent, meaning that both sides of an equation have the same units. This technique is fundamental in verifying the correctness of quotations, deriving new relationships, and identifying potential errors. For example, ensuring that the units on both sides of Newton’s second law (F=ma) match confirms that the equation is dimensionally consistent and physically meaningful.
Application of derived units:
Some applications of derived units are given below:
Joule(J):
This unit are used for heat, energy, and work. Their application in physics is given below:
Mechanics: the work which is done by a person or an object can be measured in joules. This concept is also used to understand the potential and the kinetic energy.
Thermodynamics: according to the first law of thermodynamics the energy that can be expressed in joules can't be created or can’t be destroyed and the energy in the form of heat can always be measured in joules.
Electricity: in the electrical system the energy which can be used in the form of electricity can be measured in joules because work is also done in it.
Watt(W):
These units are used for power, their application in physics are given below:
Mechanical systems: the power that can be consumed in engines or different mechanical systems can be measured in watts.
Electrical engineering: in our daily life or households like bulbs, ovens, and other electronic devices, the electric energy that can be consumed is measured in watts.
Thermodynamics: In cars engines, and other electronic devices which consume electrical energy can be measured in watts.
Volt(V):
These units are used to measure electric potential, and their application in physics is given below:
Power distribution: the voltages that can be distributed to the power line can be measured in volts.
Electronics: the electrical devices like capacitors, diodes, and others that can distribute the voltages. These voltages which can be distributed are measured in volts.
Electric circuits: in electric circuits, the potential that can be distributed is measured in volts.
Tesla(T):
These units are used to measure the magnetic flux density, their applications in physics are given below:
Physics research: In physics research when high magnetic fields are used then these field strengths can be measured in teslas.
Electromagnetism: the magnetic field strength in the magnets can be measured through teslas.
Medical imaging: In the medical field medical devices like MRI machines have also a strong magnetic field which can also be measured in teslas.
Ohm(Ω):
This unit is used to measure electric resistance, their applications in physics are given below:
Thermistor: temperature-sensitive resistors use temperature and resistance both and to measure or control the temperature ohm is used.
Circuit design: in electrical circuits where electric current is passed resistance is also present to measure the resistance we can use ohm.
Material science: to manufacture the electronic device, an ohm is used to measure the resistance.
Henry(H):
This unit is used to measure inductance, their applications in physics are given below:
Radiofrequency: In radio when the tune is played then the frequencies are matched because during their manufacturing frequencies are measured in hertz.
Electrical engineering: To make inductors and coils of inductance to make a strong magnetic field Henry is used to measure the inductance.
Power supply: to supply the power current smoothly without changing in current and voltage inductors are used.
Farad(F):
This unit is used to measure capacitance, their applications in physics are given below:
Energy storage: capacitors which are used in electrical devices are used to store energy and the farad is used to measure the capacitance of a capacitor.
Communication systems: In television, radios, and other electronic devices capacitors are used to store energy.
Newton(N):
This unit is used to measure force, their applications in physics are given below:
Aerospace: Newton is used to find or determine the thrust and friction that are produced by engines during flight.
Classic mechanics: Newton is used to determine the forces that are produced by an object or a person. Newton also presented 3 laws.
Engineering: the engineers who build the buildings and bridges calculate the forces to ensure that these can bear stress or not.
Pascal(P):
This unit is used to measure pressure, applications of Pascal are given below:
Engineering: The engineer used Pascal to calculate the stresses of the material and then used the material.
Fluid dynamics: Blood pressure, atmospheric pressure, and all fluid pressure can be measured and calculated through Pascal.
Meteorology: to measure the climate and weather Pascal is used.
Coulomb(C):
This unit is used to measure electrical charge, their application in physics are given below:
Capacitors: capacitors are used in electrical devices to store energy and to maintain the current flow.
Electrostatics: in the electrostatic experiments coulomb are used to measure the electric charge that flows through them.
Batteries: in batteries, the charge stored that is used after completing the charging.
Conclusion:
Derived units are used in various fields to measure complex quantities and physical phenomena that can't be measured by using the base quantities. Derived units like joule, watt, kelvin, coulomb, Pascal, and all others are derived from basic seven base units in the form of exponent. Now derived units are used in modern technology and sciences. Scientists used these units to measure the different quantities precisely and accurately. From time to time, the SI system can also continue to adopt the changes and present more suitable and precise units for the measurement of the quantities. The SI system adopts many changes in its units and redefines them.



