The first law of thermodynamics is also known as the Conservation of energy Principle. I will explain what is energy principle is and the following are some important points of the Energy Principle:
The energy principle can be described as the following equation:
Ein-Eout=∆E
I will exemplify the energy equation through a simple example. For instance, the rock fell from the cliff and while falling from the cliff the rock gained speed and the speed doubled while coming down. The potential energy is converted into kinetic energy as the rock is falling from height. Here the air resistance is negligible here. All these factors confirm the conservation of energy principle.
One of the simple examples of the Conservation of Energy Principle in our daily life is the man who has a lot of energy i.e. the input. If he eats junk and gains weight and the energy will be stored in the form of fat also he exercises less and that is the output. But on the other, a man who eats less has less input and ultimately loses weight. So his input is small as compared to the output.
The conservation of energy principle states that
The change in energy content of a system is equal to the difference between the energy input and output.
If the mass, energy or other quantity enters the system from outside to the system and exists in the system. But if the quantity moves within the system then it is not considered to be a transferred quantity. So it is important to understand the boundaries of the system.
In a closed system, the energy can change to heat transfer and work transfer. In this case, the conservation of energy of the close system equation will be expressed as follows:
Qnet in+Wnet in=dEsysdt
The value of the net heat transfer rate is as follows:
Qnet in=Qin-Qout
The value of net power output is as follows:
Wnet in=W in-Wout
Here dEsysdt is the rate of change of the total energy content of the system.
In the case of a compressible system, the equation of total energy consists f internal kinetic and potential energies and the equation is as follows:
e=u+K.E+P.E
e=u+V22+gz
Energy Transfer by Heat
The energy transfer by heat is one of the important topics of the energy equation. The following are some of the important key points related to the energy transfer by heat:
The heat is in the form of a latent form of internal energy.
Heat transfer is defined as the movement of thermal energy by means of nature and the temperature is decreased in this case. So the transfer of thermal energy from one system to another due to temperature variations is known as the transfer of heat.
In the case of heat transfer, the heat is always transferred from a body of higher temperature to a body of lower temperature. When both temperatures maintain equal temperature then the process of transfer stops. In the case of bodies having equal temperature, there is no transferring of heat.
Adiabatic process is the one in which there is no transfer of heat. The system is said to be in adiabatic if the system is insulted and if the system and the surroundings are at the same temperature.
The adiabatic process is confused with the isothermal process. But there is no transfer of heat but in the adiabatic process, the temperature can be changed by the work transfer.
Energy Transfer by Work
The energy transfer by work is also an important part of the energy equation. The following are some of the important key points related to energy transfer by work:
The energy interacts and results in the work.
The time rate of doing work is called the power and the power is denoted by the W.
The energy is increased when the work-consuming devices transfer energy to the fluid. A simple example of transferring energy is an electric fan. This moves the electric energy is converted into mechanical energy and this mechanical energy operates the motor of the fan and that motor starts the blades and the fan starts. But here we can say that energy is transferred and this energy transfer has no relation to the temperature.
The system has various kinds of transferring of work and the total work equation is as follows:
Wtotal=Wshaft+Wpressure+Wviscous+Wother
Shaft Work
The shaft work is also one of the important part of energy equation. So following are some of the important key points related to the shaft work:
Machines such as turbines, pump, fans or compressors all have shaft and the work protrudes through the control surface by the shaft is known as shaft work.
The equation of the shaft work is as follows:
Wshaft=ωTshaft
Wshaft=2πnTshaft
Here omega is the angular speed of the shaft and n is the number of revolutions of the shaft per unit time.
Work Done by Pressure Forces
The work done by the pressure forces is also one of the important topic that comes under the energy equation. So following are some important key points related to the work done by pressure forces:
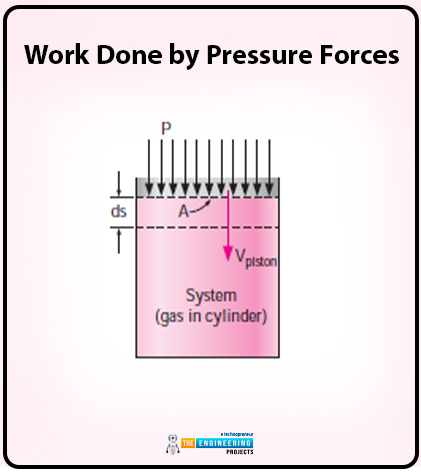
In the case of work done by pressure forces, let us consider a gas that is compressed in a piston cylinder.
The diagram of gas compression in a piston cylinder is as follows:
The piston is moved at some distance and that differential distance is ds. The differential distance is under the effect of pressure forces PA where A is the cross sectional area of the piston whereas P is the pressure forces. Here the work is being done.
The equation for work done on the system is as follows:
Wpressure= δWboundry=PAVpiston
Here the value of Vpistonis as follows:
Vpiston=dsdt
We will start the derivation with a little theoretical background.
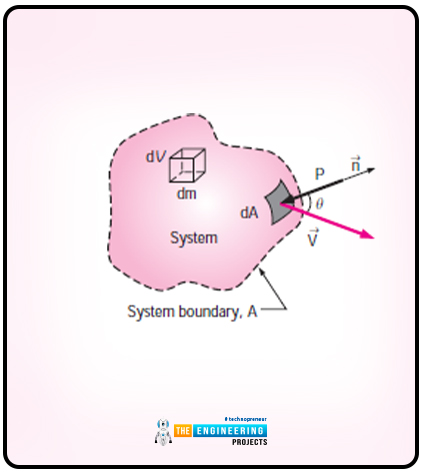
Let us consider a system that has arbitrary shape and the diagram is as follows:
The system moves with the effect of pressure. The pressure here acts in an inward direction and normal the surface. The equation for the time rate at which work is done by pressure on the differential part of the system is as follows:
Wpressure=-PdAVn
Wpressure=-PdA(V.n)
The equation for the normal component is as follows:
Vn=Vcos
Vn=V.n
So now I will show you the equation for the total rate of work done by the pressure forces:
Wpressure net in=-∫A P (V.n)=-∫APρ(V.n)dA
Now there is an equation that shows the general form of energy equation that is applied to the fixed, moving and deforming control volumes as follows:
Qnet in+Wshaft, net in+Wpressure, net in=ddt∫cvedV+∫cse(Vr.n)dA
So is the energy equation for the fixed, moving and deformed control volumes.