In this article, I will cover one of the essential topics of fluid mechanics as the title shows three crucial topics—the first concerns the conservation of mass and how it plays a critical role in our daily life. The next one involves the conservation of kinetic and potential energy and is all about the flow energy of a fluid stream. The Bernoulli equation is all about considering the energies, handling them of fluid, and neglecting the viscous forces. The last topic is energy equations, which is about the conservation of energy principle. As we know that while dealing with energy in fluid mechanics, the mechanical energy can be separated from the thermal energy and end, considering it an energy loss.
So without wasting time, let us start the article with the mass.
Conservation Laws
I will start with the laws of conservation. As you have heard about many laws, while discussing things related to mass, it is essential to examine the conservation laws. So let us discuss conservation laws one by one.
Conservation of Mass
The definition of the law of conservation of mass is as follows:
In any close or isolated system, matter cannot be created nor destroyed but can be changed and conserved.
Some of the essential key points related to the law of conservation of mass are as follows:
In the system, the mass remains constant throughout, and the according to the equation it says:
msys=constant
dmsysdt = 0
Here, dmsysdt is the mass change r within the system boundaries.
so, in the case of the control volume, the conservation of mass in terms of rate form is presented as follows:
min-mout=dmcvdt
here, the min is the total rate of control volume;l volume, and similarly, mout is the mass flow rate out of control volume
Also, dmcvdt is the mass change rate within the control volume.
You might have heard that the conservation of mass is interrelated with the continuity equation. So the conservation of mass defined in terms of the differential control volume is called Continuity Equation.
Conservation of Momentum
The definition of the law of conservation of momentum is as follows:
The Law of Conservation of Momentum states that the momentum of an isolated system is constant.
Some of the essential key points related to the law of conservation of momentum are as follows:
In fluid dynamics, the conservation of momentum is interrelated to Newton’s Law of motion. In solid mechanics, Newton’s Laws of motion are implemented.
As we know, that momentum formula is about the product of mass and velocity.
Newton’s second law of motion says:
The rate of change of momentum of the body is equal to net forces acting on it.
Conservation of Energy
The statement of conservation of energy is as follows:
The net energy transfers to or from the system during a process be equal to the change in energy content of the system.
Some of the essential key points related to the conservation of energy are as follows:
As we know that energy cannot be created nor destroyed, but it can be transformed from one state to another. So the statement of Conservation of energy is similar as it says that the energy transferred to the system is equal to the change in the system's content. So it means that no energy is destroyed it is transformed into another form.
The energy balance equation of conservation of energy will be:
Ein-Eout=dEcvdt
Here, Ein and Eout are the total energy in and out of the control volume.
dEcvdt is the rate of change energy within the control volume.
Conservation of Mass
It is the first part of the article, and while discussing this topic, we should know that it is one of the most fundamental principles in nature. At the start of the article, I have given you a brief introduction about the conservation of mass, the statement, and the energy balance equation.
Now I will discuss those key points not discussed before in detail. So their explanation is as follows:
The mass has a much similar property as the energy. One of the significant statements is that it cannot be created or destroyed. But mass can be converted to energy and vice versa with the help of the following statement and i.e.
E=mc2
Yes, you guessed it right. This is Einstein Equation. Where c is the speed of light, and the value is c=2.9979108m/s.
The equation helps us detect the change in mass whenever there is a change in energy.
As the statement of the conservation of mass shows that the system’s mass remains constant but in the case of a closed system. While discussing the control volumes, there might be some changes. The significant change will be that mass can cross boundaries.
Mass and Volume Flow Rates
These two words are well known in fluid mechanics, so readers should know these two when discussing the conservation of mass. So the definition of mass flow rate is as follows:
The mass flow through any cross-section per unit time is called mass flow rate.
Some of the essential key points related to the mass flow rate are as follows:
The fluid passing through any cross-sectional area has a flow rate. Let us suppose it passes through some small area; then, the differential mass flow rate will be:dAc.
Then, the equation will be like this:
m=ρVndAc
Here, is used for quantities such as heat, work, and mass transfer, whereas d ( differential quantity) is used for the properties.
Let us have the flow of fluid passing through some annulus with inner radius as r1 and outer radius r2 as then the equation will be:
12dAc=Ac2-Ac1=π(r22-r12)
Also, we know that the total mass flow rate is as follows:
12m=mtotal
After the integration, the mass flow rate equation will be as follows:
m=∫Ac δm = ∫Ac ρVndAc
The equation is very informative but is not used in daily life because of the integration. So the flow rates are values taken as average. The importance of density and velocity varies accordingly to the size of the pipe. Due to non-slip conditions, the value of velocity varies
So the equation of average velocity is as follows
Vavg=1Ac∫AcVndAc
In the case of compressible and incompressible flows when the density is uniform throughout the cross-sectional area, then the equation will be:
m=ρVavgAc
Volume Flow Rate
The definition of volume flow rate is as follows:
The volume of fluid flowing through any cross-section per unit of time is known as the volume flow rate.
Some of the important critical points related to the volume flow rate are as follows:
The equation of volume flow rate is as follows:
V=∫AcVndAc
V=VavgAc
V=VAc
One of the essential points that should be kept while dealing with the volume flow rate is that it should not be confused with the symbol Q as it also presents the flow rate.
There is a relation between the mass and volume flow rate, and that relation is explained by the equation.
m=ρV=Vv
Conservation of Mass Principle
The statement of conservation of mass principle is as follows:
The newt mass transfer to or from a control volume during the interval of time is equal to the net change in total mass within the boundaries of the control volume.
Equation of conservation of Mass Principle
The theoretical equation is as follows:
(Total mass entering the CV during ∆t) – (Total mass leaving CV during ∆t)
=
(Net change in mass within the Control Volume during ∆t)
The mathematical equation will be as follows:
min-mout=∆mcv
This equation can also be expressed in terms of rate form:
min-mout=dmcvdt
Here one of the essential vita points that must be kept in mind is that the conservation of mass principle is performed within the control volume boundaries.
Derivation of Conservation of Mass Principle
The theory and the mathematical equations about the conservation of mass principle are as follows:
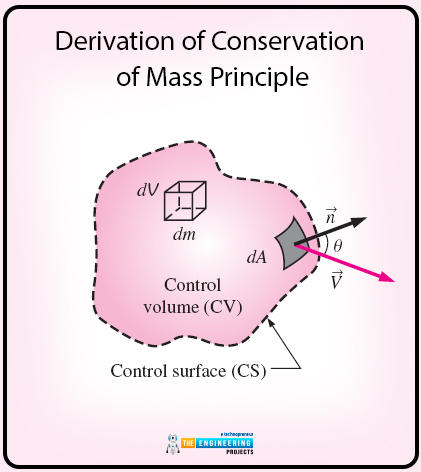
First of all, we will consider the control volume of irregular shape as shown in the diagram below:

So the mass of differential volume that is in the control volume will be:
dm=ρdV
The equation of total mass within the control volume will be:
mcv=∫cvdV
Now I will show you the equation of the rate of change of mass within the boundary of a control volume:
dmcvdt=ddt∫cvρdV
The conservation of mass principle has a special case in which no mass can cross the boundary. We can conclude that control volume restrictions are much similar to the closed system. The equation of conservation of mass principle, in this case, will be as follows:
dmcvdt=0
Now we will further assume that the mass is flowing from the differential area of the control volume. Here the unit vector will be n of differential area (dA). V will be the flow velocity and this whole theory is presented in the diagram that is mentioned above.
There is an angle at a point where the velocity can intersect the differential area.
The mass flow rate here is proportional to the normal component of velocity as:
Vn=Vcos
here there are some values of theta that are applied to the above-mentioned equation. Such as =0 when the outflow is maximum and the flow is normal to the differential area. The value of =90° when the flow is tangent to the differential area and the outflow is minimal to zero. The value of =180 when inflow is maximum and the flow and differential area is opposite to each other also the flow is normal to the differential area.
So the equation of the normal component of velocity will be as follows:
Vn=Vcos =V.n
As this is the important principle of fluid mechanics, it comprises equation many. Now there is the equation of differential mass flow rate in which the mass flow rate passing through the differential area is directly proportional to the fluid density and it is normal to the flow area:
m=ρVndA=ρVcos dA=ρV.ndA
Now there is an equation of net mass flow rate and it is an overall equation of control volume in which the flow rate moves in and out through the control surface. So the equation is as follows:
mnet=∫csm=∫csVndA=∫csρ(V.n)dA
Here are some important values of theta as we know that V.n = Vcos so the value will be <90° in the case of outflow and it will be >90° in the case of inflow. So whenever the value of the net mass flow rate is positive, it shows that it is an outflow; whenever the value is negative, it shows that the net flow is inflow.
Now there was an equation at the start which was min-mout=dmcvdt
We will rearrange it and will present it as an equation of general conservation of mass equation and it is as follows:
ddt∫cvρdV+∫csρ(V.n)dA=0
For your convenience I will explain the above equation to you. The above equation says that the rate of change of mass within the boundary of control volume along with the net mass flow rate through the control surface is said to be equal to zero.
We can also derive the equation with the help of Reynold’s Transport Theorem.
Now I will show you our second last equation and this is associated with the above equation. What we will do is we will spill the above equation into two main parts.
One part comprises the outgoing flow streams and the value will be positive. The second part comprises the incoming streams and the value will be negative. So the equation will be as follows:
ddt∫cvρdV+t∫AVndA-in∫AVndA = 0
Here A is the area of outlet and inlet and the summation value shows all the collective values of inlet and outlet.
Now moving toward, the last equation will be the end of this topic. In the last equation I will show you how mass flow rate can be shown in some different equations:
ddt∫cvρdV=inm -outm
or
dmcvdt=inm -outm
Mass Balance for Steady-Flow Processes
This topic also comes under the conservation of mass of principle. So the essential key points are as follows:
Whenever there is a steady flow, the total mass within the boundary of the control volume remains constant.
But when we have studied the conservation of mass principle it says that the mass that is entering the control volume should be equal to the mass leaving it.
Toto explain further I will unquote an example that says that while watering our flowers with the help of a garden hose. The water passing through the nozzle of the garden hose is moving in a steady motion. So the water entering the nozzle per unit time equals the water leaving per unit time.
While dealing with the steady flow, the amount of mass is not considered rather the mass flow per unit time is always considered. And that amount of mass flowing per unit time is the mass flow rate.
In the case of steady flows, the flow's inlet and outlet are always considered equal. Such as shown in the diagram.
inm =outm
There are numerous mechanical devices in which a single stream with one outlet and inlet are used. Examples are turbines, diffusers and pumps. So to have an equation for them to calculate the steady flow the equation will be as follows:
m1=m2 1V1A1=2V2A2
Here 1present the inlet of flow and 2 presents the outlet of flow.
Special Case: Incompressible Flow
Now here comes the last topic of conservation of mass principle in this topic we observe a special case study. So without wasting any time let’s have a look at the important key points:
In the case of liquids, when the fluid is compressible the conservation of mass has a defined line.
The equation for the steady and the incompressible flow will be as follows:
in =out
Here the density is cancelled from the side. So in the case of single stream, steady and incompressible flow, the equation will be as follows:
1=2=V1A1=V2A2
We have a detailed explanation of the conservation of mass but after this equation, you might have questions in your mind about the conservation of volume. So for your information, there is no such thing exists as the conservation of volume.
In the case of steady flow, the volume flow rate at the inlet and the outlets are different and may vary from device to device.
To clarify this point let us take an example of an air compressor. The volume flow rate at the outlet is less as compared to the inlet. As the mass flow rate at the inlet and outlet is constant. The reason for this is that there is a high density of air at the exit of the compressor.
In the case of steady flow, the mass flow rate along with the volume flow rate is the same or constant throughout the whole process.
so that is a whole detailed discussion about the first part of this article which covers almost every domain. So now I will start the second part of the article, which is about the Bernoulli Equation. Without wasting any time let us start.



