
Hey peeps, welcome to The Engineering Projects. We are talking about matrices, and if you want to learn them from scratch, you must go to the introduction to matrices in MATLAB. Today, we are learning how to perform different arithmetic operations on matrices. You will also see some interesting commands that are only applicable to the matrices. Here, it is important to notice that in MATLAB, the matrices are performed in the command window and there is no need to have the programming skills to perform them. Even if you are new to programming, you can easily perform the operations in MATLAB. We’ll discuss different basic operations on the matrices and will also perform each of them in MATLAB. Most of them are urinary operations and some of them are binary. Here is a small glimpse of today’s topics:
What is a matrix?
What are some basic operations of matrices?
What is an identity matrix?
How can we use the simple commands of MATLAB to perform complex and time-taking calculations with matrices?
An Introduction to Matrices
We all know what matrices are matrices. Yet, it is important to learn the basic definition of the matrices because this will create a map of how the basic operations on the matrices are performed. So, a matrix is defined as:
“A matrix is a two-dimensional array with entries of the same kind in the form of real or complex data, and it takes the shape of an ordered rectangular array surrounded by a square bracket.”
The thing to notice here is, that the data present in the matrices are of the same kind and therefore, we can perform a simple operation on each of the entries by simply applying it at once to the whole matrix.
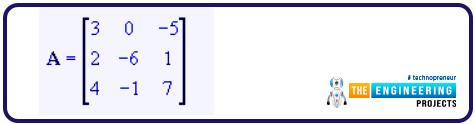
Now, have a look at the basic operations on the matrices.
Basic Operations on the Matrices
There are several operations that can be performed on the matrices. Some of them are unary operations ( those operations that require only one matrix for the application) and most of them are binary operations that require two matrices for the performance. When you observe different types of each of them, we are going through the definition of each of them, and at the end, you will also practice each of them in MATLAB. So, have a look at the definition of each of them.
The Addition of the Matrices
Yes, as you can guess, addition is a binary function, and you need two matrices to perform the addition of the matrices. The addition of the matrix takes place when both of the matrices have the same number of rows and columns. Each entry is added to the corresponding entry of the other matrix, and in this way, we get the resultant matrix with the same number of rows and columns.
One must keep in mind that addition is a commutative operation, which means if we have two matrices named A and B, respectively, then the addition process follows the rule given below:
A+B=B+A
All other rules are the same as the simple addition, but here, the equal number of rows and columns of the matrix is an additional rule that must be followed.
Subtraction of the Matrices
As with the addition, the subtraction of the matrices is a binary operation, it requires the same order of both the matrices and does not follow the commutative rule. It means:
A-B!=B-A
And that makes sense. During the subtraction of B from A, the element on B at a particular location is subtracted from the element present on the corresponding entry of A. So, if the value of this particular element is less than the element subtracted from it, we get the answer in minus. Therefore, subtraction is not commutative.
Multiplication of the Matrices
The multiply operation in the matrices is somehow a little bit different from the normal multiplication. Two types of multiplication occur in the matrices:
Multiplying the whole matrix with a scalar
Multiplying two matrices
Multiplying a single number with the whole matrix is called scalar multiplication. If we are multiplying a number k with the matrix, the multiplication of k with the matrix provides us with a resultant matrix that has each entry having the value k times more than before multiplication.
On the other hand, when two matrices are multiplied, the key point to remember is:
During the multiplication of two matrices A and B, the number of rows of matrix A must be equal to the number of columns of matrix B; otherwise, the multiplication is impossible.
Hence, if you are asked to multiply the matrices, this must be the first condition that you check. So, here is the procedure of matrix multiplication.
Check the number of rows and columns of matrices A and B.
Multiply each element of row 1 of matrix A with the column of matrix B.
Add all the results of this multiplication together.
Now, repeat the same procedure with the other rows of matrix A with the columns of matrix B.
In the end, you will get the resultant matrix that has the same number of rows as matrix A.
Therefore, the multiplication of the matrix is non-commutative and therefore we can say:
AxB!=BxA
This will be more clear when you learn the example in the next section.
Basic Operations on Matrix in MATLAB
The solutions to the operations that we have mentioned above are time taking and require a number of steps to be followed. The same results, but in a better manner, can be obtained with the help of MATLAB. Just follow the steps to perform these operations in MATLAB.
Fire up your MATLAB software.
Go to the command window.
Start writing the following code to make a matrix A in the command window:
A=[ 2 5 8; 1 8 2; 4 6 9]
The resultant matrix will be shown on the screen.
Now write the following code just below the matrix formed before:
B=[1 5 2; 4 8 9; 2 7 3]
The same result will be shown for matrix B.
Now, to perform the addition of matrix A and B, write the following command in the command window:
A+B
It will show the results.
Now write A-B.
You will get the results.
If you are performing all the operations according to the instructions, your screen will look like the following image:

For the multiplication of both types, there are different commands. For the scalar multiplication, we are using the simple command given next:
2*A
It will provide us with a matrix that has two times the values of matrix A.
For the multiplication of two matrices, the command A.*B is used. Here, the question arises why we are using the dot in between the A and B. Have a look at the results of the different types of multiplication. We have mentioned the results when we used this command and a simple command of multiplication as A*B.

Both types have different results. It is because using a dot between the A and B tells the compiler that we want the multiplication of each element with the other, and in this way, the authentic procedure for the multiplication is used as we have mentioned above in the multiplication section.
Similarly, we are testing the same condition while we want the square of the matrix. We all know that a square means that each and every value is multiplied by itself. On the other hand, if we simply apply a formula to multiply value 2 with the whole matrix, we’ll get the double of each value but not the square. Let’s see this in action in MATLAB.

You can clearly examine the difference between all the values. If we want to have the square of each element of matrix A, we have to use the third command with a dot between the matrices' names.
Identity Matrix
In the discussion in the previous lecture, when we were talking about the types of matrices, we mentioned a type called the identity matrix. It is the matrix that has the arrangement of elements in such a way that only diagonal values are 1, and all the other values in the matrix are zero. It is an interesting type of matrix, and when talking about the procedure for having an identity matrix in MATLAB, it is more interesting. The following command is used to make an identity matrix:
eye(x,y)
Where,
x=number of columns
y=numbers of rows
So basically, we are just telling the size of the matrix and MATLAB provides us with the result in a second, according to our wish. It may seem that it is a less common type of matrix, but that is not true. For many calculations, where the long and time-taking data is to be converted into a relatively simple identity matrix is used. It is also useful in systems where only binary data is used for calculations. There are some other uses of the identity matrix, but we are not going to discuss them because they are out of the scope of this lecture.
Let’s see this in MATLAB:

Interesting Commands Related to Matrix in MATLAB
MATLAB provides us with great ease in dealing with the matrices and we can use them to easily get quick and easy access to our data. So go to the command window of your MATLAB again and run the following commands on it. It's fun. To compile all the things into just one table, we have added the commands that have been discussed in the early sections of this lecture.

Command |
Description |
A=[1 3 6; 4 8 2; 6 11 3] |
It forms a matrix with the name A which has three rows and three columns with the same entries mentioned in the bracket. |
A(2,1) |
It provides us with the elements present in the second row and third column. |
size(A) |
It shows us the size of matrix A, which is the number of rows and columns, respectively. |
length(A) |
It is used to know the maximum number of rows or columns. It provides us with only one number, either of the rows or columns, which has the maximum value among two. |
A(:) |
It is the way to convert the whole matrix into a single column with all the entries one after the other in a vertical manner. |
A(:,2)=[ ] |
It is used to delete the 2nd column (or any other that is specified) and show the resultant matrix. |
A(1,:)=[ ] |
It deletes the first row and second column, then provides us with a matrix having the remaining entries. |
ones(2,4) |
It results in a matrix that contains two rows and four columns, but all the entries are one. |
A’ |
It is used to get the complement of the matrix A. |
These are some very basic commands that are related to the information that we have provided you till now. A great number of commands are also associated with the matrices in MATLAB, and we are going to discuss most of them in our discussion, but it is not possible to cover all of them in a single lecture.
Thus, today we learned a lot about matrices. We have observed some very basic but specific actions that are only possible when data is in the form of matrices. It was interesting to know that we could easily perform long calculations in MATLAB with the help of simple commands in no time. We have seen some interesting commands in MATLAB with detailed descriptions. We have also examined the output at each and every step. There are some other functions of MATLAB that help us get the results of complex commands in seconds. You must practice more by changing the elements or the numbers of rows and columns and check what results from you get with the same commands. In our next lecture, we have a lot of information about matrices.






